
【題目】若數列{an}和{bn}的項數均為n,則將 ![]() 定義為數列{an}和{bn}的距離.
定義為數列{an}和{bn}的距離.
(1)已知 ![]() ,bn=2n+1,n∈N* , 求數列{an}和{bn}的距離dn .
,bn=2n+1,n∈N* , 求數列{an}和{bn}的距離dn .
(2)記A為滿足遞推關系 ![]() 的所有數列{an}的集合,數列{bn}和{cn}為A中的兩個元素,且項數均為n.若b1=2,c1=3,數列{bn}和{cn}的距離大于2017,求n的最小值.
的所有數列{an}的集合,數列{bn}和{cn}為A中的兩個元素,且項數均為n.若b1=2,c1=3,數列{bn}和{cn}的距離大于2017,求n的最小值.
(3)若存在常數M>0,對任意的n∈N* , 恒有 ![]() 則稱數列{an}和{bn}的距離是有界的.若{an}與{an+1}的距離是有界的,求證:
則稱數列{an}和{bn}的距離是有界的.若{an}與{an+1}的距離是有界的,求證: ![]() 與
與 ![]() 的距離是有界的.
的距離是有界的.
【答案】
(1)解:數列{an}和{bn}的前n項和分別為2n+1﹣2,n2+2n,
∴dn= ![]() =|2n+1﹣2﹣n2﹣2n|,
=|2n+1﹣2﹣n2﹣2n|,
當n=1,21+1﹣2﹣12﹣2×1=﹣1
當n=2時,22+1﹣2﹣22﹣2×2=﹣2
當n=3時,23+1﹣2﹣32﹣2×3=﹣1
當n=4時,24+1﹣2﹣42﹣2×4=6,
∴dn= ![]() =|2n+1﹣2﹣n2﹣2n|=
=|2n+1﹣2﹣n2﹣2n|= ![]()
(2)解:設a1=p,其中p≠0,且p≠±1,由 ![]() ,
,
∴a2= ![]() ,a3=﹣
,a3=﹣ ![]() ,a4=
,a4= ![]() ,a5=p,
,a5=p,
∴a1=a5,
因此A中數列的項周期性重復,且間隔4項重復一次,
數列{bn}中, ![]() ,
,
數列{cn}中, ![]() ,
,
∵ ![]()
∴項數n越大,數列{bn}和{cn}的距離越大.
∵ ![]() ,
,
而 ![]() =
= ![]() ,|c1﹣b1|=1,|c2﹣b2|=1
,|c1﹣b1|=1,|c2﹣b2|=1
因此,當n=3457時, ![]() ,當n=3458時,
,當n=3458時, ![]() ,
,
故n的最小值為3458
(3)證明:∵{an}與{an+1}的距離是有界的,
∴存在正數M,對任意的n∈N*,有|an﹣an﹣1|+|an﹣1+an﹣2|+…+|a2﹣a1|≤M,
∵|an|=|an﹣an﹣1+an﹣1+an﹣2+…+a2﹣a1+a1|≤|an﹣an﹣1|+|an﹣1+an﹣2|+…+|a2﹣a1|+|a1|≤|M+|a1|,
記|≤|M+|a1|,則有|an+12﹣an2|=|(an+1﹣an)(an+1+an)|≤|an+1﹣an|(|an+1|+|an|)≤2K|an+1﹣an|,
∴|an+12﹣an2|+|an2﹣an﹣12|+…+|a22﹣a12|≤2KM,
故 ![]() 與
與 ![]() 的距離是有界的
的距離是有界的
【解析】(1)數列{an}和{bn}的前n項和分別為2n+1﹣2,n2+2n,根據新定義求出即可;(2)由數列的遞推公式,即可求得a2 , a3 , a4 , a5 , 求得A中數列的項周期性重復,且間隔4項重復一次,求得數列{bn}和{cn}規律,可知隨著項數n越大,數列{bn}和{cn}的距離越大,由 ![]() ,根據周期的定義,求得n的最大值;(3)根據新定義結合絕對值不等式,即可證明.
,根據周期的定義,求得n的最大值;(3)根據新定義結合絕對值不等式,即可證明.


科目:高中數學 來源: 題型:
【題目】已知函數f(x)=|x﹣1|+|x﹣a|
(1)若函數f(x)的值域為[2,+∞),求實數a的值
(2)若f(2﹣a)≥f(2),求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,在三棱錐A﹣BCD中,側面ABD,ACD是全等的直角三角形,AD是公共的斜邊且AD= ![]() ,BD=CD=1,另一側面ABC是正三角形.
,BD=CD=1,另一側面ABC是正三角形. 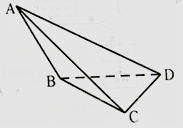
(1)求證:AD⊥BC;
(2)若在線段AC上存在一點E,使ED與平面BCD成30°角,試求二面角A﹣BD﹣E的大小.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(已知函數f(x)=|2x+1|+|x﹣2|,不等式f(x)≤2的解集為M.
(1)求M;
(2)記集合M的最大元素為m,若正數a,b,c滿足abc=m, 求證: ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】中國“一帶一路”戰略構思提出后, 某科技企業為抓住“一帶一路”帶來的機遇, 決定開發生產一款大型電子設備, 生產這種設備的年固定成本為![]() 萬元, 每生產
萬元, 每生產![]() 臺,需另投入成本
臺,需另投入成本![]() (萬元), 當年產量不足
(萬元), 當年產量不足![]() 臺時,
臺時,![]() (萬元); 當年產量不小于
(萬元); 當年產量不小于![]() 臺時
臺時![]() (萬元), 若每臺設備售價為
(萬元), 若每臺設備售價為![]() 萬元, 通過市場分析,該企業生產的電子設備能全部售完.
萬元, 通過市場分析,該企業生產的電子設備能全部售完.
(1)求年利潤![]() (萬元)關于年產量
(萬元)關于年產量![]() (臺)的函數關系式;
(臺)的函數關系式;
(2)年產量為多少臺時 ,該企業在這一電子設備的生產中所獲利潤最大?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】據統計,截至2016年底全國微信注冊用戶數量已經突破9.27億,為調查大學生這個微信用戶群體中每人擁有微信群的數量,現從某市大學生中隨機抽取100位同學進行了抽樣調查,結果如下:
微信群數量(個) | 頻數 | 頻率 |
0~4 | 0.15 | |
5~8 | 40 | 0.4 |
9~12 | 25 | |
13~16 | a | c |
16以上 | 5 | b |
合計 | 100 | 1 |
(Ⅰ)求a,b,c的值及樣本中微信群個數超過12的概率;
(Ⅱ)若從這100位同學中隨機抽取2人,求這2人中恰有1人微信群個數超過12的概率;
(Ⅲ)以(1)中的頻率作為概率,若從全市大學生中隨機抽取3人,記X表示抽到的是微信群個數超過12的人數,求X的分布列和數學期望E(X).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知D=  ,給出下列四個命題:
,給出下列四個命題:
P1:(x,y)∈D,x+y+1≥0;
P2:(x,y)∈D,2x﹣y+2≤0;
P3:(x,y)∈D, ![]() ≤﹣4;
≤﹣4;
P4:(x,y)∈D,x2+y2≤2.
其中真命題的是( )
A.P1 , P2
B.P2 , P3
C.P2 , P4
D.P3 , P4
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】
(2015·新課標Ⅱ)設函數f‘(x)是奇函數f(x)(x![]() R)的導函數,f(-1)=0,當x
R)的導函數,f(-1)=0,當x![]() 0時,xf'(x)-f(x)
0時,xf'(x)-f(x)![]() 0,則使得f(x)
0,則使得f(x)![]() 0成立的x的取值范圍是()
0成立的x的取值范圍是()
A.(-![]() ,-1)
,-1)![]() (0,1)
(0,1)
B.(-1,0)![]() (1,+
(1,+![]() )
)
C.(-![]() ,-1)
,-1)![]() (-1,0)
(-1,0)
D.(0,1)![]() (1,+
(1,+![]() )
)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com