
已知拋物線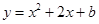
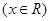 與坐標軸有三個交點,經過這三點的圓記為
與坐標軸有三個交點,經過這三點的圓記為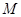 .
.
(1)求實數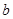 的取值范圍;
的取值范圍;
 (2)設拋物線與x軸的交點從左到右分別為A、B,與y軸的交點為C,求A、B、C三點的坐標;
(2)設拋物線與x軸的交點從左到右分別為A、B,與y軸的交點為C,求A、B、C三點的坐標;
(3)設直線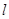 是拋物線在點A處的切線,試判斷直線
是拋物線在點A處的切線,試判斷直線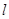 是否也是圓
是否也是圓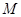 的切線?并說明理由.
的切線?并說明理由.
直線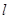 不可能是圓
不可能是圓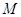 的切線.
的切線.
【解析】解:(1)∵拋物線與坐標軸有三個交點∴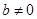 ,否則拋物線與坐標軸只有兩個交點,與題設不符,由
,否則拋物線與坐標軸只有兩個交點,與題設不符,由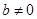 知,拋物線與y軸有一個非原點的交點
知,拋物線與y軸有一個非原點的交點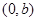 ,故拋物線與x軸有兩個不同的交點,即方程
,故拋物線與x軸有兩個不同的交點,即方程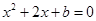 有兩個不同的實根
有兩個不同的實根
∴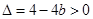 即
即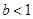
∴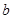 的取值范圍是
的取值范圍是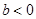 或
或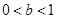 -----------------------------------3分
-----------------------------------3分
(2)令x=0得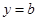 ,∴
,∴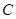
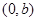 ---------------------------------4分
---------------------------------4分
令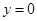 得
得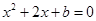 解得
解得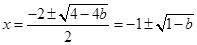
∴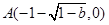 ,
,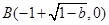 ------------------------------6分
------------------------------6分
(3)解法1:∵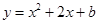 ∴
∴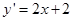
∴直線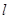 的斜率
的斜率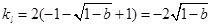 -----------------------7分
-----------------------7分
∵圓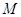 過A、B、C三點,∴圓心M為線段AB與AC的垂直平分線的交點
過A、B、C三點,∴圓心M為線段AB與AC的垂直平分線的交點
∵AB的垂直平分線即拋物線的對稱軸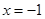
∵線段AC的中點為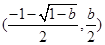 直線AC的斜率
直線AC的斜率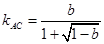
∴線段AC的垂直平分線方程為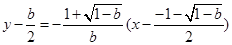 ---(
---( )----10分
)----10分
將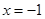 代入(
代入(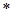 )式解得
)式解得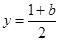 ,即
,即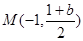 ------------------------11分
------------------------11分
∴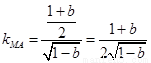 ,若直線
,若直線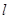 也是圓
也是圓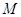 的切線,則
的切線,則
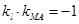 即
即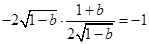
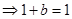 解得
解得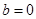
這與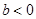 或
或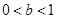 矛盾 ----------------------------------------13分
矛盾 ----------------------------------------13分
∴直線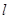 不可能是圓
不可能是圓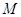 的切線. -----------------------------------14分
的切線. -----------------------------------14分
解法2:∵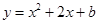 ∴
∴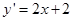
∴直線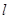 的斜率
的斜率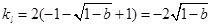 ---------------------------7分
---------------------------7分
設圓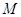 的方程為
的方程為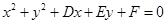
∵圓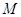 過
過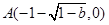 ,
,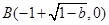 ,
,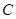
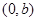
∴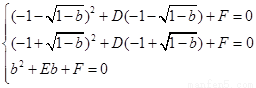 解得
解得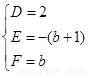 ------------10分
------------10分
∴圓心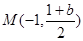 -------------------------------------------------11分
-------------------------------------------------11分
∴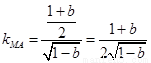 ,若直線
,若直線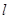 也是圓
也是圓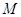 的切線,則
的切線,則
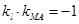 即
即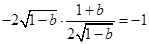
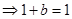 解得
解得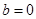
這與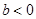 或
或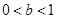 矛盾----------------------------------------13分
矛盾----------------------------------------13分
∴直線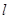 不可能是圓
不可能是圓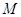 的切線.-----------------------------------14分
的切線.-----------------------------------14分


科目:高中數學 來源: 題型:
| ||
| 2 |
| 2 |
| ||
| 2 |
| 24 |
| 25 |
查看答案和解析>>
科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源: 題型:
已知拋物線![]()
![]() 與坐標軸有三個交點,經過這三點的圓記為
與坐標軸有三個交點,經過這三點的圓記為![]() .
.
(1) 求實數![]() 的取值范圍;
的取值范圍;
(2) 設拋物線與x軸的交點從左到右分別為A、B,與y軸的交點為C,求A、B、C三點的坐標;
(3) 設直線![]() 是拋物線在點A處的切線,試判斷直線
是拋物線在點A處的切線,試判斷直線![]() 是否也是圓
是否也是圓![]() 的切線?并說明理由.
的切線?并說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com