
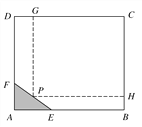
【題目】如圖所示,為了保護環境,實現城市綠化,某房地產公司要在拆遷地長方形ABCD處規劃一塊長方形地面HPGC,建造住宅小區公園,但不能越過文物保護區三角形AEF的邊線EF.已知AB=CD=200 m,BC=AD=160 m,AF=40 m,AE=60 m,問如何設計才能使公園占地面積最大,求出最大面積.
【答案】詳見解析.
【解析】試題分析: 在EF上取一點P,作PH⊥BC,PG⊥CD,垂足分別為H、G,設PH=x,則140≤x≤200.
由三角形相似得出PG用x表示,進而得出公園占地面積關于x的函數,用配方法得出函數的最值,以及取到最值時的x值.
試題解析:
如題圖,在EF上取一點P,作PH⊥BC,PG⊥CD,垂足分別為H、G,設PH=x,則140≤x≤200.
由三角形相似性質PG=120+![]() (200-x),
(200-x),
∴公園占地面積為S=x[120+![]() (200-x)]
(200-x)]
=-![]() x2+
x2+![]() x
x
=-![]() (x-190)2+
(x-190)2+![]() ×1902(140≤x≤200),
×1902(140≤x≤200),
∴當x=190時,Smax=![]() m2.
m2.
答:在EF上取一點P,使P到BC距離為190m時,公園PHCG占地面積最大,最大面積為![]() m2.
m2.
點睛: 本題考查函數的實際應用問題,解決問題的關鍵是利用相似求出函數的解析式,用二次函數的單調性解決函數的最值.解決函數模型應用的解答題,還有以下幾點容易造成失分:①讀不懂實際背景,不能將實際問題轉化為函數模型.②對涉及的相關公式,記憶錯誤.③在求解的過程中計算錯誤.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】通過研究學生的學習行為,專家發現,學生的注意力著老師講課時間的變化而變化,講課開始時,學生的興趣激增;中間有一段時間,學生的興趣保持較理想的狀態,隨后學生的注意力開始分散,設f(t)表示學生注意力隨時間t(分鐘)的變化規律\left(f(t)越大,表明學生注意力越集中),經過實驗分析得知: 
(1)講課開始后多少分鐘,學生的注意力最集中?能持續多少分鐘?
(2)講課開始后5分鐘與講課開始后25分鐘比較,何時學生的注意力更集中?
(3)一道數學難題,需要講解24分鐘,并且要求學生的注意力至少達到180,那么經過適當安排,教師能否在學生達到所需的狀態下講授完這道題目?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在三棱柱ABCA1B1C1中,已知AB⊥側面BB1C1C,AB=BC=1,BB1=2,∠BCC1=![]() .
.
(1)求證:C1B⊥平面ABC;
設![]() (0≤λ≤1),且平面AB1E與BB1E所成的銳二面角的大小為30°,
(0≤λ≤1),且平面AB1E與BB1E所成的銳二面角的大小為30°,
試求λ的值.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】函數f(x)是定義在[-1,0)∪(0,1]上的奇函數,當x∈[-1,0)時,f(x)=2x+![]() (x∈R).
(x∈R).
(1)當x∈(0,1]時,求f(x)的解析式.
(2)判斷f(x)在(0,1]上的單調性,并證明你的結論.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在如圖所示的圓臺中,![]() 是下底面圓
是下底面圓![]() 的直徑,
的直徑,![]() 是上底面圓
是上底面圓![]() 的直徑,
的直徑,![]() 是圓臺的一條母線.
是圓臺的一條母線.
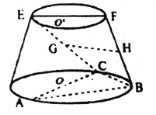
(Ⅰ)已知![]() ,
,![]() 分別為
分別為![]() ,
,![]() 的中點,求證:
的中點,求證:![]() 平面
平面![]() ;
;
(Ⅱ)已知![]() ,
,![]() ,求二面角
,求二面角![]() 的余弦值
的余弦值
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com