
(1)若![]() =5
=5![]() ,求直線l的斜率;
,求直線l的斜率;
(2)證明M、N兩點的縱坐標之積為-![]() a2.
a2.
(1)解:設P(x1,y1),Q(x2,y2),因為雙曲線的離心率為![]() ,?
,?
所以c=![]() a,b=
a,b=![]() a,雙曲線方程為2x2-y2=
a,雙曲線方程為2x2-y2=
因為![]() =5
=5![]() ,所以x2=
,所以x2=![]() c. ?
c. ?
因為直線l:y=k(x-c),?
所以y2=-![]() . ?
. ?
點Q是雙曲線上一點,所以2(![]() )2-(-
)2-(-![]() )2=
)2=
整理,得![]() e2-
e2-![]() e2k2=2,解得k=±
e2k2=2,解得k=±![]() . ?
. ?
(2)證明:設P(x1,y1),Q(x2,y2),?
由已知AP:y=![]() (x+a),AQ:y=
(x+a),AQ:y=![]() (x+a),?
(x+a),?
所以ym=![]() (
(![]() +a),yn==
+a),yn==![]() (
(![]() +a). ?
+a). ?
所以ymyn=![]() ·
·![]() (
(![]() +a)2=
+a)2=![]() (
(![]() +a)2.?
+a)2.?
由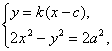 得(2-k2)x2+2k2cx-k
得(2-k2)x2+2k2cx-k
所以x1+x2=![]() ,x1x2=
,x1x2=![]() ,?
,?
y1y2=k2(x1-c)(x2-c)=k2[x1x2-c(x1+x2)+c2]=k2![]() , ?
, ?
x1x2+a(x1+x2)+a2=k2![]() . ?
. ?
所以ymyn=![]() ·
·![]() =-
=-![]() a2.
a2.


 課堂全解字詞句段篇章系列答案
課堂全解字詞句段篇章系列答案 步步高口算題卡系列答案
步步高口算題卡系列答案 點睛新教材全能解讀系列答案
點睛新教材全能解讀系列答案 小學教材完全解讀系列答案
小學教材完全解讀系列答案科目:高中數學 來源: 題型:
雙曲線C:![]() -
-![]() =1(a>b>0)中,F1、F2是它的焦點,設拋物線l的焦點與雙曲線C的右焦點F2重合,l的準線與C的左準線重合,P是C與l的一個交點,那么
=1(a>b>0)中,F1、F2是它的焦點,設拋物線l的焦點與雙曲線C的右焦點F2重合,l的準線與C的左準線重合,P是C與l的一個交點,那么![]() =______________.
=______________.
查看答案和解析>>
科目:高中數學 來源:2013-2014學年人教版高考數學文科二輪專題復習提分訓練24練習卷(解析版) 題型:選擇題
已知雙曲線C1: -
- =1(a>0,b>0)的離心率為2.若拋物線C2:x2=2py(p>0)的焦點到雙曲線C1的漸近線的距離為2,則拋物線C2的方程為( )
=1(a>0,b>0)的離心率為2.若拋物線C2:x2=2py(p>0)的焦點到雙曲線C1的漸近線的距離為2,則拋物線C2的方程為( )
(A)x2=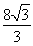 y (B)x2=
y (B)x2= y
y
(C)x2=8y (D)x2=16y
查看答案和解析>>
科目:高中數學 來源:2011-2012學年江西省高三第一次統考理科數學 題型:選擇題
已知拋物線x2=2py(p>0)與雙曲線 -
-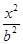 =1(a>0, b>0)有相同的焦點F,點B是兩曲線的一
=1(a>0, b>0)有相同的焦點F,點B是兩曲線的一
個交點,且BF⊥y軸,若L為雙曲線的一條漸近線,則L的傾斜角所在的區間可能是 ( )
A.(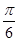 ,
,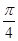 ) B.(
) B.(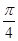 ,
,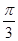 ) C.(
) C.( ,
,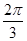 ) D.(
) D.(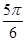 ,π)
,π)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com