
【題目】已知動圓![]() 恒過點
恒過點![]() ,且與直線
,且與直線![]() 相切.
相切.
(1)求圓心![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(2)設![]() 是軌跡
是軌跡![]() 上橫坐標為2的點,
上橫坐標為2的點,![]() 的平行線
的平行線![]() 交軌跡
交軌跡![]() 于
于![]() ,
,![]() 兩點,交軌跡
兩點,交軌跡![]() 在
在![]() 處的切線于點
處的切線于點![]() ,問:是否存在實常數
,問:是否存在實常數![]() 使
使![]() ,若存在,求出
,若存在,求出![]() 的值;若不存在,說明理由.
的值;若不存在,說明理由.
【答案】(1)![]() ;(2)存在,
;(2)存在,![]() .
.
【解析】
(1)根據拋物線的定義,容易知其軌跡為拋物線;結合已知點的坐標,即可求得方程;
(2)由拋物線方程求得點![]() 的坐標,設出直線
的坐標,設出直線![]() 的方程,利用導數求得點
的方程,利用導數求得點![]() 的坐標,聯立直線
的坐標,聯立直線![]() 的方程和拋物線方程,結合韋達定理,求得
的方程和拋物線方程,結合韋達定理,求得![]() ,進而求得
,進而求得![]() 與
與![]() 之間的大小關系,即可求得參數
之間的大小關系,即可求得參數![]() .
.
(1)由題意得,點![]() 與點
與點![]() 的距離始終等于點
的距離始終等于點![]() 到直線
到直線![]() 的距離,
的距離,
由拋物線的定義知圓心![]() 的軌跡是以點
的軌跡是以點![]() 為焦點,直線
為焦點,直線![]() 為準線的拋物線,
為準線的拋物線,
則![]() ,
,![]() .∴圓心
.∴圓心![]() 的軌跡方程為
的軌跡方程為![]() .
.
(2)因為![]() 是軌跡
是軌跡![]() 上橫坐標為2的點,
上橫坐標為2的點,
由(1)不妨取![]() ,所以直線
,所以直線![]() 的斜率為1.
的斜率為1.
因為![]() ,所以設直線
,所以設直線![]() 的方程為
的方程為![]() ,
,![]() .
.
由![]() ,得
,得![]() ,則
,則![]() 在點
在點![]() 處的切線斜率為2,
處的切線斜率為2,
所以![]() 在點
在點![]() 處的切線方程為
處的切線方程為![]() .
.
由![]() 得
得![]() 所以
所以![]() ,
,
所以![]() .
.
由![]() 消去
消去![]() 得
得![]() ,
,
由![]() ,得
,得![]() 且
且![]() .
.
設![]() ,
,![]() ,
,
則![]() ,
,![]() .
.
因為點![]() ,
,![]() ,
,![]() 在直線
在直線![]() 上,
上,
所以![]() ,
,![]() ,
,
所以![]()
![]()
![]() ,
,
所以![]() .
.
∴![]()
故存在![]() ,使得
,使得![]() .
.


 亮點激活精編提優100分大試卷系列答案
亮點激活精編提優100分大試卷系列答案科目:高中數學 來源: 題型:
【題目】隨著現代社會的發展,我國對于環境保護越來越重視,企業的環保意識也越來越強.現某大型企業為此建立了5套環境監測系統,并制定如下方案:每年企業的環境監測費用預算定為1200萬元,日常全天候開啟3套環境監測系統,若至少有2套系統監測出排放超標,則立即檢查污染源處理系統;若有且只有1套系統監測出排放超標,則立即同時啟動另外2套系統進行1小時的監測,且后啟動的這2套監測系統中只要有1套系統監測出排放超標,也立即檢查污染源處理系統.設每個時間段(以1小時為計量單位)被每套系統監測出排放超標的概率均為![]() ,且各個時間段每套系統監測出排放超標情況相互獨立.
,且各個時間段每套系統監測出排放超標情況相互獨立.
(1)當![]() 時,求某個時間段需要檢查污染源處理系統的概率;
時,求某個時間段需要檢查污染源處理系統的概率;
(2)若每套環境監測系統運行成本為300元/小時(不啟動則不產生運行費用),除運行費用外,所有的環境監測系統每年的維修和保養費用需要100萬元.現以此方案實施,問該企業的環境監測費用是否會超過預算(全年按9000小時計算)?并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖是某地區2000年至2016年環境基礎設施投資額![]() (單位:億元)的折線圖.則下列結論中表述不正確的是( )
(單位:億元)的折線圖.則下列結論中表述不正確的是( )
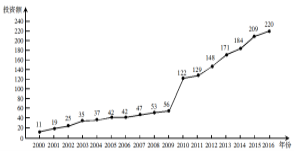
A. 從2000年至2016年,該地區環境基礎設施投資額逐年增加;
B. 2011年該地區環境基礎設施的投資額比2000年至2004年的投資總額還多;
C. 2012年該地區基礎設施的投資額比2004年的投資額翻了兩番 ;
D. 為了預測該地區2019年的環境基礎設施投資額,根據2010年至2016年的數據(時間變量t的值依次為![]() )建立了投資額y與時間變量t的線性回歸模型
)建立了投資額y與時間變量t的線性回歸模型![]() ,根據該模型預測該地區2019的環境基礎設施投資額為256.5億元.
,根據該模型預測該地區2019的環境基礎設施投資額為256.5億元.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
:![]() (
(![]() )的左、右焦點分別為
)的左、右焦點分別為![]() ,
,![]() ,以原點為圓心,橢圓的短半軸長為半徑的圓與直線
,以原點為圓心,橢圓的短半軸長為半徑的圓與直線![]() 相切,點
相切,點![]() 在橢圓
在橢圓![]() 上,
上,![]() ,
,![]() ,
,
(1)求橢圓![]() 的方程;
的方程;
(2)若直線![]() :
:![]() 與橢圓交于
與橢圓交于![]() ,
,![]() 兩點,點
兩點,點![]() ,若
,若![]() ,求斜率
,求斜率![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=x-lnx,g(x)=x2-ax.
(1)求函數f(x)在區間[t,t+1](t>0)上的最小值m(t);
(2)令h(x)=g(x)-f(x),A(x1,h(x1)),B(x2,h(x2))(x1≠x2)是函數h(x)圖像上任意兩點,且滿足![]() >1,求實數a的取值范圍;
>1,求實數a的取值范圍;
(3)若x∈(0,1],使f(x)≥![]() 成立,求實數a的最大值.
成立,求實數a的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在最新公布的湖南新高考方案中,“![]() ”模式要求學生在語數外3門全國統考科目之外,在歷史和物理2門科目中必選且只選1門,再從化學、生物、地理、政治4門科目中任選2門,后三科的高考成績按新的規則轉換后計入高考總分.相應地,高校在招生時可對特定專業設置具體的選修科目要求.雙超中學高一年級有學生1200人,現從中隨機抽取40人進行選科情況調查,用數字1~6分別依次代表歷史、物理、化學、生物、地理、政治6科,得到如下的統計表:
”模式要求學生在語數外3門全國統考科目之外,在歷史和物理2門科目中必選且只選1門,再從化學、生物、地理、政治4門科目中任選2門,后三科的高考成績按新的規則轉換后計入高考總分.相應地,高校在招生時可對特定專業設置具體的選修科目要求.雙超中學高一年級有學生1200人,現從中隨機抽取40人進行選科情況調查,用數字1~6分別依次代表歷史、物理、化學、生物、地理、政治6科,得到如下的統計表:
序號 | 選科情況 | 序號 | 選科情況 | 序號 | 選科情況 | 序號 | 選科情況 |
1 | 134 | 11 | 236 | 21 | 156 | 31 | 235 |
2 | 235 | 12 | 234 | 22 | 235 | 32 | 236 |
3 | 235 | 13 | 145 | 23 | 245 | 33 | 235 |
4 | 145 | 14 | 135 | 24 | 235 | 34 | 135 |
5 | 156 | 15 | 236 | 25 | 256 | 35 | 156 |
6 | 245 | 16 | 236 | 26 | 156 | 36 | 236 |
7 | 256 | 17 | 156 | 27 | 134 | 37 | 156 |
8 | 235 | 18 | 236 | 28 | 235 | 38 | 134 |
9 | 235 | 19 | 145 | 29 | 246 | 39 | 235 |
10 | 236 | 20 | 235 | 30 | 156 | 40 | 245 |
(1)雙超中學規定:每個選修班最多編排50人且盡量滿額編班,每位老師執教2個選修班(當且僅當一門科目的選課班級總數為奇數時,允許這門科目的1位老師只教1個班).已知雙超中學高一年級現有化學、生物科目教師每科各8人,用樣本估計總體,則化學、生物兩科的教師人數是否需要調整?如果需要調整,各需增加或減少多少人?
(2)請創建列聯表,運用獨立性檢驗的知識進行分析,探究是否有![]() 的把握判斷學生“選擇化學科目”與“選擇物理科目”有關.
的把握判斷學生“選擇化學科目”與“選擇物理科目”有關.
附: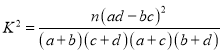
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
(3)某高校![]() 在其熱門人文專業
在其熱門人文專業![]() 的招生簡章中明確要求,僅允許選修了歷史科目,且在政治和地理2門中至少選修了1門的考生報名.現從雙超中學高一新生中隨機抽取3人,設具備
的招生簡章中明確要求,僅允許選修了歷史科目,且在政治和地理2門中至少選修了1門的考生報名.現從雙超中學高一新生中隨機抽取3人,設具備![]() 高校
高校![]() 專業報名資格的人數為
專業報名資格的人數為![]() ,用樣本的頻率估計概率,求
,用樣本的頻率估計概率,求![]() 的分布列與期望.
的分布列與期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設三棱錐![]() 的每個頂點都在球
的每個頂點都在球![]() 的球面上,
的球面上,![]() 是面積為
是面積為![]() 的等邊三角形,
的等邊三角形,![]() ,
,![]() ,且平面
,且平面![]() 平面
平面![]() .
.
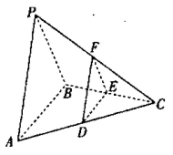
(1)確定![]() 的位置(需要說明理由),并證明:平面
的位置(需要說明理由),并證明:平面![]() 平面
平面![]() .
.
(2)與側面![]() 平行的平面
平行的平面![]() 與棱
與棱![]() ,
,![]() ,
,![]() 分別交于
分別交于![]() ,
,![]() ,
,![]() ,求四面體
,求四面體![]() 的體積的最大值.
的體積的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com