分析:(1)根據橢圓的方程,算出a=5、b=3且c=4,△PF
1F
2中利用中位線定理,結合橢圓的定義即可證出PF
1的中點M滿足關系式
|MO|=5-|PF1|;
(2)設|PF
1|=t
1,|PF
2|=t
2,根據橢圓的定義和勾股定理建立關于t
1、t
2的方程組,平方相減即可求出|PF
1|•|PF
2|=18,結合直角三角形面積公式即可算出△F
1PF
2的面積;
(3)設P(x,y),根據△F
1PF
2的面積S
△ F1PF2=•2c•|y|=9,解出y=±
,再代入橢圓方程求出橫坐標的值,即可得到P點的坐標.
解答:解:∵橢圓方程為
+=1,
∴a=5,b=3,可得c=
=4
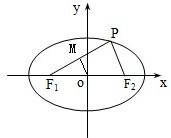
(1)∵△PF
1F
2中,O、M分別是PF
1、F
1F
2的中點
∴|OM|=
|PF
2|,根據橢圓的定義得|PF
2|=10-|PF
1|
因此,|OM|=
|PF2|=5-|PF1|;
(2)設|PF
1|=t
1,|PF
2|=t
2,則t
1+t
2=10①
又∵Rt△PF
1F
2中,利用勾股定理得
+=(2c)2=82②,
由①
2-②,得t
1t
2=18
∴△F
1PF
2的面積S
△ F1PF2=t1t2=9;
(3)設P(x,y),由S
△ F1PF2=•2c•|y|=4•|y|,
得4|y|=9,解之得
|y|=⇒y=±,
將
y=±代入橢圓方程解,得
x=±,
∴P點的坐標為
P(,±)或
P(-,±).
點評:本題給出橢圓的焦點三角形為直角三角形,求它的面積和直角頂點P的坐標,著重考查了勾股定理、橢圓的定義和簡單幾何性質等知識,屬于基礎題.




 課前課后同步練習系列答案
課前課后同步練習系列答案 課堂小作業系列答案
課堂小作業系列答案 黃岡小狀元口算速算練習冊系列答案
黃岡小狀元口算速算練習冊系列答案 成功訓練計劃系列答案
成功訓練計劃系列答案 倍速訓練法直通中考考點系列答案
倍速訓練法直通中考考點系列答案 如圖,已知點P為橢圓
如圖,已知點P為橢圓 (2012•奉賢區二模)已知:P為橢圓
(2012•奉賢區二模)已知:P為橢圓