
 ,烏克蘭隊贏的概率為
,烏克蘭隊贏的概率為 ,且每局比賽輸贏互不影響.若中國隊第n局的得分記為an,令Sn=a1+a2+…+an.
,且每局比賽輸贏互不影響.若中國隊第n局的得分記為an,令Sn=a1+a2+…+an. ,烏克蘭隊贏的概率為
,烏克蘭隊贏的概率為 ,且每局比賽輸贏互不影響.若中國隊第n局的得分記為an,令Sn=a1+a2+…+an.
,且每局比賽輸贏互不影響.若中國隊第n局的得分記為an,令Sn=a1+a2+…+an. 即為烏克蘭隊輸的概率,同理,烏克蘭隊贏的概率
即為烏克蘭隊輸的概率,同理,烏克蘭隊贏的概率 即為中國隊輸的概率,兩隊和棋的概率為
即為中國隊輸的概率,兩隊和棋的概率為 ,又每局比賽輸贏互不影響,
,又每局比賽輸贏互不影響,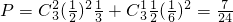 ;
;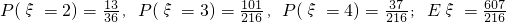 .
. 即為烏克蘭隊輸的概率,同理,烏克蘭隊贏的概率
即為烏克蘭隊輸的概率,同理,烏克蘭隊贏的概率 即為中國隊輸的概率,兩隊和棋的概率為
即為中國隊輸的概率,兩隊和棋的概率為 ,又每局比賽輸贏互不影響,而比賽規則規定贏一局得2分,平一局得1分,輸一局得0分,
,又每局比賽輸贏互不影響,而比賽規則規定贏一局得2分,平一局得1分,輸一局得0分,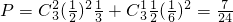 ;
;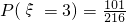 .
. ,即為烏克蘭隊輸的概率,同理烏克蘭隊贏的概率
,即為烏克蘭隊輸的概率,同理烏克蘭隊贏的概率 即為中國隊輸的概率,和棋的概率為
即為中國隊輸的概率,和棋的概率為 ,又每局比賽輸贏互不影響.若中國隊第n局的得分記為an,令Sn=a1+a2+…+an 所以S3=4及進行3場比賽得分和為4,又比賽規則規定贏一局得2分,平一局得1分,輸一局得0分,所以進行3場比賽得4分的所有可能為:①3場比賽中國隊贏2場,輸1場;②3場比賽中國隊贏1場,平兩場;利用獨立事件同時發生的概率公式即可求得;
,又每局比賽輸贏互不影響.若中國隊第n局的得分記為an,令Sn=a1+a2+…+an 所以S3=4及進行3場比賽得分和為4,又比賽規則規定贏一局得2分,平一局得1分,輸一局得0分,所以進行3場比賽得4分的所有可能為:①3場比賽中國隊贏2場,輸1場;②3場比賽中國隊贏1場,平兩場;利用獨立事件同時發生的概率公式即可求得;  ,即為烏克蘭隊輸的概率,同理烏克蘭隊贏的概率
,即為烏克蘭隊輸的概率,同理烏克蘭隊贏的概率 即為中國隊輸的概率,和棋的概率為
即為中國隊輸的概率,和棋的概率為 ,又每局比賽輸贏互不影響.若中國隊第n局的得分記為an,令Sn=a1+a2+…+an 所以S3=4及進行3場比賽得分和為4,又比賽規則規定贏一局得2分,平一局得1分,輸一局得0分,所以進行3場比賽得4分的所有可能為:①3場比賽中國隊贏2場,輸1場;②3場比賽中國隊贏1場,平兩場;利用獨立事件同時發生的概率公式即可求得;
,又每局比賽輸贏互不影響.若中國隊第n局的得分記為an,令Sn=a1+a2+…+an 所以S3=4及進行3場比賽得分和為4,又比賽規則規定贏一局得2分,平一局得1分,輸一局得0分,所以進行3場比賽得4分的所有可能為:①3場比賽中國隊贏2場,輸1場;②3場比賽中國隊贏1場,平兩場;利用獨立事件同時發生的概率公式即可求得; 

 超能學典應用題題卡系列答案
超能學典應用題題卡系列答案科目:高中數學 來源: 題型:
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
查看答案和解析>>
科目:高中數學 來源:2011年湖北省荊州市松滋二中高考數學限時訓練(解析版) 題型:解答題
 ,烏克蘭隊贏的概率為
,烏克蘭隊贏的概率為 ,且每局比賽輸贏互不影響.若中國隊第n局的得分記為an,令Sn=a1+a2+…+an.
,且每局比賽輸贏互不影響.若中國隊第n局的得分記為an,令Sn=a1+a2+…+an. ,烏克蘭隊贏的概率為
,烏克蘭隊贏的概率為 ,且每局比賽輸贏互不影響.若中國隊第n局的得分記為an,令Sn=a1+a2+…+an.
,且每局比賽輸贏互不影響.若中國隊第n局的得分記為an,令Sn=a1+a2+…+an.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com