
【題目】定義“正對數”:ln+x= ![]() ,現有四個命題: ①若a>0,b>0,則ln+(ab)=bln+a
,現有四個命題: ①若a>0,b>0,則ln+(ab)=bln+a
②若a>0,b>0,則ln+(ab)=ln+a+ln+b
③若a>0,b>0,則 ![]() b
b
④若a>0,b>0,則ln+(a+b)≤ln+a+ln+b+ln2
其中的真命題有: . (寫出所有真命題的編號)
【答案】①③④
【解析】解:對于①,當0<a<1,b>0時,有0<ab<1,從而ln+(ab)=0,bln+a=b×0=0,
∴ln+(ab)=bln+a;
當a≥1,b>0時,有ab>1,從而ln+(ab)=lnab=blna,bln+a=blna,
∴ln+(ab)=bln+a;
∴當a>0,b>0時,ln+(ab)=bln+a,命題①正確;
對于②,當a= ![]() 時,滿足a>0,b>0,而ln+(ab)=ln+
時,滿足a>0,b>0,而ln+(ab)=ln+ ![]() =0,ln+a+ln+b=ln+
=0,ln+a+ln+b=ln+ ![]() +ln+2=ln2,
+ln+2=ln2,
∴ln+(ab)≠ln+a+ln+b,命題②錯誤;
對于③,由“正對數”的定義知,ln+x≥0且ln+x≥lnx.
當0<a<1,0<b<1時,ln+a﹣ln+b=0﹣0=0,而ln+ ![]() ≥0,
≥0,
∴ ![]() b.
b.
當a≥1,0<b<1時,有 ![]() ,ln+a﹣ln+b=ln+a﹣0=ln+a,而ln+
,ln+a﹣ln+b=ln+a﹣0=ln+a,而ln+ ![]() =ln
=ln ![]() =lna﹣lnb,
=lna﹣lnb,
∵lnb<0,
∴ ![]() b.
b.
當0<a<1,b≥1時,有0< ![]() ,ln+a﹣ln+b=0﹣ln+b=﹣ln+b,而ln+
,ln+a﹣ln+b=0﹣ln+b=﹣ln+b,而ln+ ![]() =0,
=0,
∴ ![]() b.
b.
當a≥1,b≥1時,ln+a﹣ln+b=lna﹣lnb=ln ![]() ,則
,則 ![]() b.
b.
∴當a>0,b>0時, ![]() b,命題③正確;
b,命題③正確;
對于④,由“正對數”的定義知,當x1≤x2時,有 ![]() ,
,
當0<a<1,0<b<1時,有0<a+b<2,從而ln+(a+b)<ln+2=ln2,ln+a+ln+b+ln2=0+0+ln2=ln2,
∴ln+(a+b)≤ln+a+ln+b+ln2.
當a≥1,0<b<1時,有a+b>1,從而ln+(a+b)=ln(a+b)<ln(a+a)=ln2a,
ln+a+ln+b+ln2=lna+0+ln2=ln2a,
∴ln+(a+b)≤ln+a+ln+b+ln2.
當0<a<1,b≥1時,有a+b>1,從而ln+(a+b)=ln(a+b)<ln(a+b)=ln2b,
ln+a+ln+b+ln2=0+lnb+ln2=ln2b,
∴ln+(a+b)≤ln+a+ln+b+ln2.
當a≥1,b≥1時,ln+(a+b)=ln(a+b),ln+a+ln+b+ln2=lna+lnb+ln2=ln(2ab),
∵2ab﹣(a+b)=ab﹣a+ab﹣b=a(b﹣1)+b(a﹣1)≥0,
∴2ab≥a+b,從而ln+(a+b)≤ln+a+ln+b+ln2.
命題④正確.
∴正確的命題是①③④.
所以答案是:①③④.
【考點精析】通過靈活運用命題的真假判斷與應用,掌握兩個命題互為逆否命題,它們有相同的真假性;兩個命題為互逆命題或互否命題,它們的真假性沒有關系即可以解答此題.


科目:高中數學 來源: 題型:
【題目】已知下列命題: ①x∈(0,2),3x>x3的否定是:x∈(0,2),3x≤x3;
②若f(x)=2x﹣2﹣x , 則x∈R,f(﹣x)=﹣f(x);
③若f(x)=x+ ![]() ,x0∈(0,+∞),f(x0)=1;
,x0∈(0,+∞),f(x0)=1;
④在△ABC中,若A>B,則sin A>sin B.
其中真命題是 . (將所有真命題序號都填上)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在公差不為0的等差數列{an}中,a22=a3+a6 , 且a3為a1與a11的等比中項.
(Ⅰ)求數列{an}的通項公式;
(Ⅱ)設bn=(﹣1)n ![]() ,求數列{bn}的前n項和Tn .
,求數列{bn}的前n項和Tn .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知等差數列{an}的前n項和為Sn , a1=a,當n≥2時, ![]() =3n2an+S
=3n2an+S ![]() ,an≠0,n∈N*.
,an≠0,n∈N*.
(1)求a的值;
(2)設數列{cn}的前n項和為Tn , 且cn=3n﹣1+a5 , 求使不等式4Tn>S10成立的最小正整數n的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設等差數列{an}的前n項和為Sn , 且S4=4S2 , a2n=2an+1.
(Ⅰ)求數列{an}的通項公式
(Ⅱ)設數列{bn}的前n項和為Tn , 且 ![]() (λ為常數).令cn=b2n , (n∈N*),求數列{cn}的前n項和Rn .
(λ為常數).令cn=b2n , (n∈N*),求數列{cn}的前n項和Rn .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系xOy中,曲線C1的參數方程為 ![]() (t為參數,a>0).在以坐標原點為極點,x軸正半軸為極軸的極坐標系中,曲線C2:ρ=4cosθ.
(t為參數,a>0).在以坐標原點為極點,x軸正半軸為極軸的極坐標系中,曲線C2:ρ=4cosθ.
(Ⅰ)說明C1是哪一種曲線,并將C1的方程化為極坐標方程;
(Ⅱ)直線C3的極坐標方程為θ=α0 , 其中α0滿足tanα0=2,若曲線C1與C2的公共點都在C3上,求a.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知向量 ![]() =(sin(π+ωx),2cosωx),
=(sin(π+ωx),2cosωx), ![]() =(2
=(2 ![]() sin(
sin( ![]() +ωx),cosωx),(ω>0),函數f(x)=
+ωx),cosωx),(ω>0),函數f(x)= ![]()
![]() ,其圖象上相鄰的兩個最低點之間的距離為π.
,其圖象上相鄰的兩個最低點之間的距離為π.
(Ⅰ)求函數f(x)的對稱中心;
(Ⅱ)在銳角△ABC中,角A、B、C的對邊分別為a、b、c,tanB= ![]() ,求f(A)的取值范圍.
,求f(A)的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某中學隨機選取了![]() 名男生,將他們的身高作為樣本進行統計,得到如圖所示的頻率分布直方圖,觀察圖中數據,完成下列問題.
名男生,將他們的身高作為樣本進行統計,得到如圖所示的頻率分布直方圖,觀察圖中數據,完成下列問題.
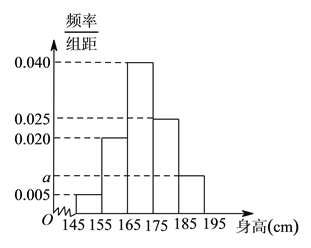
(![]() )求
)求![]() 的值及樣本中男生身高在
的值及樣本中男生身高在![]() (單位:
(單位:![]() )的人數.
)的人數.
(![]() )假設用一組中的每個數據可用該組區間的中點值代替,通過樣本估計該校全體男生的平均身高.
)假設用一組中的每個數據可用該組區間的中點值代替,通過樣本估計該校全體男生的平均身高.
(![]() )在樣本中,從身高在
)在樣本中,從身高在![]() 和
和![]() (單位:
(單位:![]() )內的男生中任選兩人,求這兩人的身高都不低于
)內的男生中任選兩人,求這兩人的身高都不低于![]() 的概率.
的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com