Question

判斷函數f(x)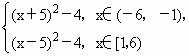＝的奇偶性．

Answer 1

答案：
解析：
提示：

分析：本題若畫出圖象，可直現形象地看出其奇偶性，但是不嚴格；利用定義判斷此函數的奇偶性，需分x∈(－6，－1]，x∈[1，6)兩種情況說明． 　　評注：(1)分段函數的奇偶性應分段證明f(－x)與f(x)的關系，只有當對稱的兩段上都滿足相同的關系時才能判斷其奇偶性． 　　(2)若證明當x∈(－6，－l]，f(－x)與f(x)的關系時，x∈(－6，－l]，則－x∈[1，6)，其中的f(－x)應將－x代入[1，6)的表達式中，得到的(x＋5)2－4＝f(x)正好是x∈(－6，－l]的表達式，若x∈[1，6)時，同理． 　　(3)若f(x)是定義在R上的奇函數時，必有f(0)＝0．