
【題目】已知函數f(x)=alnx﹣x2+1.
(Ⅰ)若曲線y=f(x)在x=1處的切線方程為4x﹣y+b=0,求實數a和b的值;
(Ⅱ)討論函數f(x)的單調性;
【答案】(Ⅰ)a=6,b=﹣4.(Ⅱ)答案見解析.
【解析】試題分析:
(1)由題意得到關于實數a,b的方程組,求解方程組可得a=6,b=﹣4.
(2)首先求解導函數,然后對參數a分類討論可得:
當a≤0時,f(x)在(0,+∞)上是減函數,
當a>0時,f(x)在![]() 上是增函數,在
上是增函數,在![]() 上是減函數.
上是減函數.
試題解析:
(Ⅰ)f(x)=alnx﹣x2+1求導得![]()
在x=1處的切線方程為4x﹣y+b=0,f′(1)=a﹣2=4,得a=6,4﹣f(1)+b=0;b=﹣4.
(Ⅱ)![]()
當a≤0時,f′(x)≤0在(0,+∞)恒成立,所以f(x)在(0,+∞)上是減函數,
當a>0時,![]() (舍負)
(舍負)![]() ,
,![]() f(x)在
f(x)在![]() 上是增函數,在
上是增函數,在![]() 上是減函數.
上是減函數.


科目:高中數學 來源: 題型:
【題目】如圖,在矩形ABCD中,AB=2BC,點M在邊DC上,點F在邊AB上,且DF⊥AM,垂足為E,若將△ADM沿AM折起,使點D位于D′位置,連接D′B,D′C得四棱錐D′﹣ABCM. 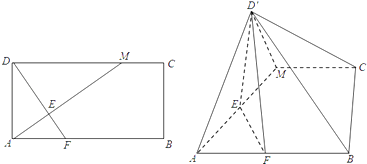
(1)求證:AM⊥D′F;
(2)若∠D′EF= ![]() ,直線D'F與平面ABCM所成角的大小為
,直線D'F與平面ABCM所成角的大小為 ![]() ,求直線AD′與平面ABCM所成角的正弦值.
,求直線AD′與平面ABCM所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓的中心在原點,焦點為![]() ,且離心率為
,且離心率為 ![]() .
.
(1)求橢圓的方程;
(2)直線(與坐標軸 不平行)與橢圓交于不同的兩點,且線段中點的橫坐標為![]() ,求直線傾斜角的取值范圍.
,求直線傾斜角的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數 ![]() ,(a為常數且a>0).
,(a為常數且a>0).
(1)若函數的定義域為 ![]() ,值域為
,值域為 ![]() ,求a的值;
,求a的值;
(2)在(1)的條件下,定義區間(m,n),[m,n],(m,n],[m,n)的長度為n﹣m,其中n>m,若不等式f(x)+b>0,x∈[0,π]的解集構成的各區間的長度和超過 ![]() ,求b的取值范圍.
,求b的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司準備將1000萬元資金投入到市環保工程建設中,現有甲、乙兩個建設項目選擇,若投資甲項目一年后可獲得的利潤![]() (萬元)的概率分布列如下表所示:
(萬元)的概率分布列如下表所示:

且![]() 的期望
的期望![]() ;若投資乙項目一年后可獲得的利潤
;若投資乙項目一年后可獲得的利潤![]() (萬元)與該項目建設材料的成本有關,在生產的過程中,公司將根據成本情況決定是否在第二和第三季度進行產品的價格調整,兩次調整相互獨立且調整的概率分別為
(萬元)與該項目建設材料的成本有關,在生產的過程中,公司將根據成本情況決定是否在第二和第三季度進行產品的價格調整,兩次調整相互獨立且調整的概率分別為![]() 和
和![]() .若乙項目產品價格一年內調整次數
.若乙項目產品價格一年內調整次數![]() (次數)與
(次數)與![]() 的關系如下表所示:
的關系如下表所示:

(1)求![]() 的值;
的值;
(2)求![]() 的分布列;
的分布列;
(3)若![]() ,則選擇投資乙項目,求此時
,則選擇投資乙項目,求此時![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一只小蜜蜂在一個棱長為3的正方體玻璃容器內隨機飛行,若蜜蜂在飛行過程中與正方體玻璃容器6個表面中至少有一個的距離不大于1,則就有可能撞到玻璃上面不安全,若始終保持與正方體玻璃容器6個表面的距離均大于1,則飛行是安全的,假設蜜蜂在正方體玻璃容器內飛行到每一位置可能性相同,那么蜜蜂飛行是安全的概率是 .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com