
【題目】已知函數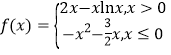 ,若方程
,若方程![]() (
(![]() 為常數)有兩個不相等的根,則實數
為常數)有兩個不相等的根,則實數![]() 的取值范圍是( )
的取值范圍是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
【答案】D
【解析】
求出當x>0時,函數的導數,研究函數的極值和圖象,作出函數f(x)的圖象,由數形結合進行求解即可.
當x>0時,函數f′(x)=2﹣(lnx+1)=1﹣lnx,
由f′(x)>0得1﹣lnx>0得lnx<1,得0<x<e,
由f′(x)<0得1﹣lnx<0得lnx>1,得x>e,當x值趨向于正無窮大時,y值也趨向于負無窮大,即當x=e時,函數f(x)取得極大值,
極大值為f(e)=2e﹣elne=2e﹣e=e,
當x≤0時,f(x)=﹣x2﹣![]() x=﹣(x+
x=﹣(x+![]() )2+
)2+![]() ,是二次函數,在軸處取得最大值
,是二次函數,在軸處取得最大值![]() ,
,
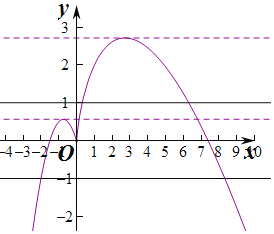
作出函數f(x)的圖象如圖:
要使f(x)=a(a為常數)有兩個不相等的實根,
則a<0或![]() <a<e,
<a<e,
即實數a的取值范圍是(﹣∞,0)∪![]() ,
,
故選:D.


科目:高中數學 來源: 題型:
【題目】若三次函數![]() (
(![]() )的圖象上存在相互平行且距離為
)的圖象上存在相互平行且距離為![]() 的兩條切線,則稱這兩條切線為一組“距離為
的兩條切線,則稱這兩條切線為一組“距離為![]() 的友好切線組”.已知
的友好切線組”.已知![]() ,則函數
,則函數![]() 的圖象上“距離為4的友好切線組”有( )組?
的圖象上“距離為4的友好切線組”有( )組?
A. 0B. 1C. 2D. 3
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某食品廠為了檢查甲、乙兩條自動包裝流水線的生產情況,隨機在這兩條流水線上各抽取100件產品作為樣本稱出它們的質量(單位:毫克),質量值落在![]() 的產品為合格品,否則為不合格品.如表是甲流水線樣本頻數分布表,如圖是乙流水線樣本的頻率分布直方圖.
的產品為合格品,否則為不合格品.如表是甲流水線樣本頻數分布表,如圖是乙流水線樣本的頻率分布直方圖.
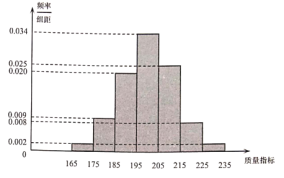
產品質量/毫克 | 頻數 |
| 3 |
| 9 |
| 19 |
| 35 |
| 22 |
| 7 |
| 5 |
(1)由以上統計數據完成下面![]() 列聯表,能否在犯錯誤的概率不超過0.15的前提下認為產品的包裝合格與兩條自動包裝流水線的選擇有關?
列聯表,能否在犯錯誤的概率不超過0.15的前提下認為產品的包裝合格與兩條自動包裝流水線的選擇有關?
甲流水線 | 乙流水線 | 總計 | |
合格品 | |||
不合格品 | |||
總計 |
附表:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(參考公式:![]() ,
,![]() )
)
(2)按照以往經驗,在每小時次品數超過180件時,產品的次品率會大幅度增加,為檢測公司的生產能力,同時盡可能控制不合格品總量,公司工程師抽取幾組一小時生產產品數據進行次品情況檢查分析,在![]() (單位:百件)件產品中,得到次品數量
(單位:百件)件產品中,得到次品數量![]() (單位:件)的情況匯總如下表所示:
(單位:件)的情況匯總如下表所示:
| 0.5 | 2 | 3.5 | 4 | 5 |
| 2 | 14 | 24 | 35 | 40 |
根據公司規定,在一小時內不允許次品數超過180件,請通過計算分析,按照公司的現有生產技術設備情況,判斷可否安排一小時生產2000件的任務?
(參考公式:用最小二乘法求線性回方程![]() 的系數公式
的系數公式
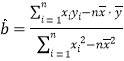
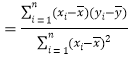 ;
;![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司為確定下一年度投入某種產品的宣傳費,需了解年宣傳費![]() (單位:萬元)對年銷售量
(單位:萬元)對年銷售量![]() (單位:噸)和年利潤
(單位:噸)和年利潤![]() (單位:萬元)的影響.對近六年的年宣傳費
(單位:萬元)的影響.對近六年的年宣傳費![]() 和年銷售量
和年銷售量![]() (
(![]() )的數據作了初步統計,得到如下數據:
)的數據作了初步統計,得到如下數據:
年份 |
|
|
|
|
|
|
年宣傳費 |
|
|
|
|
|
|
年銷售量 |
|
|
|
|
|
|
經電腦模擬,發現年宣傳費![]() (萬元)與年銷售量
(萬元)與年銷售量![]() (噸)之間近似滿足關系式
(噸)之間近似滿足關系式![]() (
(![]() ).對上述數據作了初步處理,得到相關的值如表:
).對上述數據作了初步處理,得到相關的值如表:
|
|
|
|
|
|
|
|
(1)根據所給數據,求![]() 關于
關于![]() 的回歸方程;
的回歸方程;
(2)已知這種產品的年利潤![]() 與
與![]() ,
,![]() 的關系為
的關系為![]() 若想在
若想在![]() 年達到年利潤最大,請預測
年達到年利潤最大,請預測![]() 年的宣傳費用是多少萬元?
年的宣傳費用是多少萬元?
附:對于一組數據![]() ,
,![]() ,…,
,…,![]() ,其回歸直線
,其回歸直線![]() 中的斜率和截距的最小二乘估計分別為
中的斜率和截距的最小二乘估計分別為 ,
,![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com