
【題目】已知曲線C的極坐標方程為ρ=4cosθ,以極點為原點,極軸為x軸正半軸建立平面直角坐標系,設直線l的參數方程為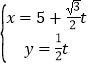 (t為參數).
(t為參數).
(1)求曲線C的直角坐標方程與直線l的普通方程;
(2)設曲線C與直線l相交于P、Q兩點,以PQ為一條邊作曲線C的內接矩形,求該矩形的面積.
科目:高中數學 來源: 題型:
【題目】某高中為了解高中學生的性別和喜歡打籃球是否有關,對50名高中學生進行了問卷調查,得到如下列聯表:

已知在這50人中隨機抽取1人,抽到喜歡打籃球的學生的概率為![]()
(Ⅰ)請將上述列聯表補充完整;
(Ⅱ)判斷是否有99.5%的把握認為喜歡打籃球與性別有關?

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知極坐標系的極點在直角坐標系的原點處,極軸與x軸的正半軸重合.直線l的參數方程為: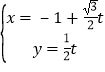 (t為參數),曲線C的極坐標方程為:ρ=4cosθ.
(t為參數),曲線C的極坐標方程為:ρ=4cosθ.
(Ⅰ)寫出C的直角坐標方程,并指出C是什么曲線;
(Ⅱ)設直線l與曲線C相交于P、Q兩點,求|PQ|值。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在直三棱柱ABC﹣A1B1C1中,AA1=AC=2AB=2,且BC1⊥A1C.
(Ⅰ)求證:平面ABC1⊥平面A1C1CA;
(Ⅱ)設D是A1C1的中點,判斷并證明在線段BB1上是否存在點E,使DE∥平面ABC1;若存在,求三棱錐E﹣ABC1的體積.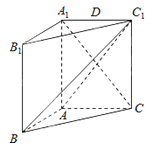
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列{an}(n=1,2,3,4,5)滿足a1=a5=0,且當2≤k≤5時,(ak﹣ak﹣1)2=1,令S=![]() , 則S不可能的值是( )
, 則S不可能的值是( )
A.4
B.0
C.1
D.-4
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列{an}前n項和Sn滿足Sn+1=a2Sn+a1 , 其中a2≠0.
(Ⅰ)求證數列{an}是首項為1的等比數列;
(Ⅱ)當a2=2時,是否存在等差數列{bn},使得a1bn+a2bn﹣1+a3bn﹣2+…+anb1=2n+1﹣n﹣2對一切n∈N*都成立?若存在,求出bn;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】現有5名男生、2名女生站成一排照相,
(1)兩女生要在兩端,有多少種不同的站法?
(2)兩名女生不相鄰,有多少種不同的站法?
(3)女生甲不在左端,女生乙不在右端,有多少種不同的站法?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com