
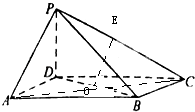
【題目】如圖,在四棱錐P﹣ABCED中,PD⊥面ABCD,四邊形ABCD為平行四邊形,∠DAB=60°,AB=PA=2AD=4, 
(1)若E為PC中點,求證:PA∥平面BDE
(2)求三棱錐D﹣BCP的體積.
【答案】
(1)證明:連結AC,BD,交于點O,
∵四邊形ABCD為平行四邊形,∴O是AC中點,
∵E是PC中點,∴OE∥AP,
又AP平面BDE,OE平面BDE,
∴PA∥平面BDE
(2)解:∵S△BDC= ![]() =2
=2 ![]() ,
,
PD= ![]() =2
=2 ![]() ,
,
∴ ![]() =
= ![]() =4.
=4.
【解析】(1)連結AC,BD,交于點O,連結OE,則OE∥AP,由此能證明PA∥平面BDE.(2)求出S△BDC= ![]() =2
=2 ![]() ,PD=
,PD= ![]() =2
=2 ![]() ,由
,由 ![]() ,能求出三棱錐D﹣BCP的體積.
,能求出三棱錐D﹣BCP的體積.
【考點精析】解答此題的關鍵在于理解直線與平面平行的判定的相關知識,掌握平面外一條直線與此平面內的一條直線平行,則該直線與此平面平行;簡記為:線線平行,則線面平行.


科目:高中數學 來源: 題型:
【題目】已知三角形的三內角A、B、C所對邊的長分別為a、b、c,設向量 ![]() ,
, ![]() ,若
,若 ![]() .
.
(1)求角B的大小;
(2)若△ABC的面積為 ![]() ,求AC邊的最小值,并指明此時三角形的形狀.
,求AC邊的最小值,并指明此時三角形的形狀.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知經銷某種商品的電商在任何一個銷售季度內,每售出![]() 噸該商品可獲利潤
噸該商品可獲利潤![]() 萬元,未售出的商品,每
萬元,未售出的商品,每![]() 噸虧損
噸虧損![]() 萬元.根據往年的銷售經驗,得到一個銷售季度內市場需求量的頻率分布直方圖如右圖所示.已知電商為下一個銷售季度籌備了
萬元.根據往年的銷售經驗,得到一個銷售季度內市場需求量的頻率分布直方圖如右圖所示.已知電商為下一個銷售季度籌備了![]() 噸該商品.現(xiàn)以
噸該商品.現(xiàn)以![]() (單位:噸,
(單位:噸, ![]() )表示下一個銷售季度的市場需求量,
)表示下一個銷售季度的市場需求量, ![]() (單位:萬元)表示該電商下一個銷售季度內經銷該商品獲得的利潤.
(單位:萬元)表示該電商下一個銷售季度內經銷該商品獲得的利潤.
(Ⅰ)根據頻率分布直方圖,估計一個銷售季度內市場需求量![]() 的平均數與中位數的大小;
的平均數與中位數的大小;
(Ⅱ)根據直方圖估計利潤![]() 不少于57萬元的概率.
不少于57萬元的概率.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲、乙兩人玩轉盤游戲,該游戲規(guī)則是這樣的:一個質地均勻的標有12等分數字格的轉盤(如圖),甲、乙兩人各轉轉盤一次,轉盤停止時指針所指的數字為該人的得分.(假設指針不能指向分界線)現(xiàn)甲先轉,乙后轉,求下列事件發(fā)生的概率 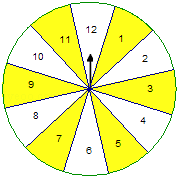
(1)甲得分超過7分的概率.
(2)甲得7分,且乙得10分的概率
(3)甲得5分且獲勝的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線C: ![]() 的焦點為F,直線
的焦點為F,直線![]() 與y軸的交點為P,與C的交點為Q,且
與y軸的交點為P,與C的交點為Q,且![]() .
.
(1)求C的方程;
(2)過F的直線![]() 與C相交于A,B兩點,若AB的垂直平分線
與C相交于A,B兩點,若AB的垂直平分線![]() 與C相較于M,N兩點,且A,M,B,N四點在同一圓上,求
與C相較于M,N兩點,且A,M,B,N四點在同一圓上,求![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,在三棱錐P -ABC中,PA⊥底面ABC,∠BCA![]() 90°,AP
90°,AP![]() AC,點D,E分別在棱PB,PC上,且BC∥平面ADE.
AC,點D,E分別在棱PB,PC上,且BC∥平面ADE.

(Ⅰ)求證:DE⊥平面PAC;
(Ⅱ)若PC⊥AD,且三棱錐P-ABC的體積為8,求多面體ABCED的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(本小題滿分12分) 某中學的環(huán)保社團參照國家環(huán)境標準制定了該校所在區(qū)域空氣質量指數與空氣質量等級對應關系如下表(假設該區(qū)域空氣質量指數不會超過![]() ):
):
空氣質量指數 |
|
|
|
|
|
|
空氣質量等級 |
|
|
|
|
|
|
該社團將該校區(qū)在![]() 年
年![]() 天的空氣質量指數監(jiān)測數據作為樣本,繪制的頻率分布直方圖如下圖,把該直方圖所得頻率估計為概率.
天的空氣質量指數監(jiān)測數據作為樣本,繪制的頻率分布直方圖如下圖,把該直方圖所得頻率估計為概率.
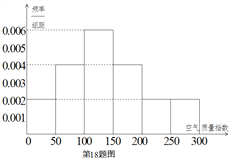
(Ⅰ)請估算![]() 年(以
年(以![]() 天計算)全年空氣質量優(yōu)良的天數(未滿一天按一天計算);
天計算)全年空氣質量優(yōu)良的天數(未滿一天按一天計算);
(Ⅱ)該校![]() 年
年![]() 月
月![]() 、
、![]() 日將作為高考考場,若這兩天中某天出現(xiàn)
日將作為高考考場,若這兩天中某天出現(xiàn)![]() 級重度污染,需要凈化空氣費用
級重度污染,需要凈化空氣費用![]() 元,出現(xiàn)
元,出現(xiàn)![]() 級嚴重污染,需要凈化空氣費用
級嚴重污染,需要凈化空氣費用![]() 元,記這兩天凈化空氣總費用為
元,記這兩天凈化空氣總費用為![]() 元,求
元,求![]() 的分布列及數學期望.
的分布列及數學期望.
查看答案和解析>>
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com