
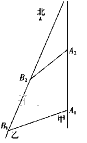
【題目】如圖,甲船以每小時30![]() 海里的速度向正北方向航行,乙船按固定方向勻速直線航行.當甲船位于A1處時,乙船位于甲船的北偏西105°方向的B1處,此時兩船相距20海里.當甲船航行20分鐘到達A2處時,乙船航行到甲船的北偏西120°方向的B2處,此時兩船相距10
海里的速度向正北方向航行,乙船按固定方向勻速直線航行.當甲船位于A1處時,乙船位于甲船的北偏西105°方向的B1處,此時兩船相距20海里.當甲船航行20分鐘到達A2處時,乙船航行到甲船的北偏西120°方向的B2處,此時兩船相距10![]() 海里,問乙船每小時航行多少海里?
海里,問乙船每小時航行多少海里?
【答案】30![]()
【解析】試題分析:解法一:連接![]() ,依題意可得
,依題意可得![]() ,求得
,求得![]() 的值,推斷出
的值,推斷出![]() 是等比三角形,進而求得
是等比三角形,進而求得![]() ,在
,在![]() 中,利用余弦定理求得
中,利用余弦定理求得![]() 的值,進而求得乙船的速度
的值,進而求得乙船的速度
解法二:連接![]() ,先計算出
,先計算出![]() ,從而得到
,從而得到![]() ,由余弦定理計算出
,由余弦定理計算出![]() ,再計算出
,再計算出![]() ,得到
,得到![]() ,解三角形求出
,解三角形求出![]() 的值
的值
解析:解法一:如圖,連結A1B2,
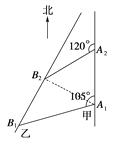
由題意知A2B2=10![]() n mile,A1A2=30
n mile,A1A2=30![]() ×
×![]() =10
=10![]() n mile.
n mile.
所以A1A2=A2B2.
又∠A1A2B2=180°-120°=60°,
所以△A1A2B2是等邊三角形.
所以A1B2=A1A2=10![]() n mile.
n mile.
由題意知,A1B1=20 n mile,∠B1A1B2=105°-60°=45°,
在△A1B2B1中,由余弦定理,得B1B=A1B+A1B-2A1B1·A1B2·cos45°=202+(10![]() )2-2×20×10
)2-2×20×10![]() ×
×![]() =200.
=200.
所以B1B2=10![]() n mile.
n mile.
因此,乙船速度的大小為![]() ×60=30
×60=30![]() (n mile/h).
(n mile/h).
答:乙船每小時航行30![]() n mile.
n mile.
解法二:如下圖所示,連結A2B1,
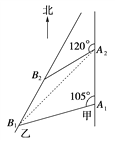
由題意知A1B1=20 n mile,A1A2=30![]() ×
×![]()
=10![]() n mile,∠B1A1A2=105°,
n mile,∠B1A1A2=105°,
又cos105°=cos(45°+60°)
=cos45°cos60°-sin45°sin60°=![]() ,
,
sin105°=sin(45°+60°)=sin45°cos60°+cos45°sin60°
=![]() ,
,
在△A2A1B1中,由余弦定理,得A2B=A1B+A1A-2A1B1·A1A2·cos105°=202+(10![]() )2-2×20×10
)2-2×20×10![]() ×
×![]() =100(4+2
=100(4+2![]() ),
),
所以A2B1=10(1+![]() )n mile
)n mile
由正弦定理,得sin∠A1A2B1=![]() ·sin∠B1A1A2=
·sin∠B1A1A2=![]() ×
×![]() =
=![]() ,
,
所以∠A1A2B1=45°,即∠B1A2B2=60°-45°=15°,cos15°=sin105°=![]() .
.
在△B1A2B2中,由題知A2B2=10![]() n mile,
n mile,
由余弦定理,得B1B=A2B+A2B-2A2B1·A2B2·cos15°=102(1+![]() )2+(10
)2+(10![]() )2-2×10(1+
)2-2×10(1+![]() )×10
)×10![]() ×
×![]() =200,
=200,
所以B1B2=10![]() n mile,故乙船速度的大小為
n mile,故乙船速度的大小為![]() ×60=30
×60=30![]() (n mile/h).
(n mile/h).
答:乙船每小時航行30![]() n mile.
n mile.


科目:高中數學 來源: 題型:
【題目】一批產品中,有一級品100個,二級品60個,三級品40個,分別用系統(tǒng)抽樣和分層抽樣的方法,從這批產品中抽取一個容量為20的樣本,寫出抽樣過程,并說明采用哪種抽樣方法更能反映總體水平.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某城市為了解游客人數的變化規(guī)律,提高旅游服務質量,收集并整理了2014年1月至2016年12月期間月接待游客量(單位:萬人)的數據,繪制了下面的折線圖.

根據該折線圖,下列結論錯誤的是( )
A. 月接待游客量逐月增加
B. 年接待游客量逐年增加
C. 各年的月接待游客量高峰期大致在7,8月
D. 各年1月至6月的月接待游客量相對于7月至12月,波動性更小,變化比較平穩(wěn)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】函數f(x)=2x3﹣9x2+12x+1的單調減區(qū)間是( )
A.(1,2)
B.(2,+∞)
C.(﹣∞,1)
D.(﹣∞,1)和(2,+∞)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列![]() ,
,![]() ,
,![]() ,
,![]() 具有性質
具有性質![]() ;對任意
;對任意![]() ,
,![]() ,
,![]() 與
與![]() 兩數中至少有一個是該數列中的一項,給出下列三個結論:
兩數中至少有一個是該數列中的一項,給出下列三個結論:
①數列![]() ,
,![]() ,
,![]() ,
,![]() 具有性質
具有性質![]() ;
;
②若數列![]() 具有性質
具有性質![]() ,則
,則![]() ;
;
③若數列![]() ,
,![]() ,
,![]() 具有性質
具有性質![]() ,則
,則![]() .
.
其中,正確結論的個數是( ).
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設f(x)是定義在R上的可導函數,且滿足f′(x)>f(x),對任意的正數a,下面不等式恒成立的是( )
A.f(a)<eaf(0)
B.f(a)>eaf(0)
C.![]()
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】假設關于某設備的使用年限x和所支出的維修費用y(單位:萬元)有如下的統(tǒng)計資料:
使用年限x/年 | 2 | 3 | 4 | 5 | 6 |
維修費用y/萬元 | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
若由資料知y對x呈線性相關關系.試求:
(1)回歸方程![]() x+
x+![]() 的系數
的系數![]() .
.
(2)使用年限為10年時,試估計維修費用是多少.
查看答案和解析>>
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com