
函數的定義是什么?如何判斷兩個函數是同一個函數呢?如何來表示一個函數呢?請根據條件使用適當的方法來表示函數y=2x2+2x.
(1)求f(1),f(2),f(-1).
(2)不通過求f(1),f(2),f(-1)比較它們的大小.
|
解:(1)由函數的解析式可以解得:f(1)=4,f(2)=12,f(-1)=0,故可用解析式來表示函數. 由題意列表得:
由上表可知:f(1)=4,f(2)=12,f(-1)=0.故可用列表來表示函數. (2)畫出函數y=2x2+2x的圖象如圖所示.
由函數y=2x2+2x的圖象可知,f(-1)<f(1)<f(2). 表示函數的方法,常用的有解析法、列表法和圖象法三種. 1.解析法:就是把兩個變量的函數關系,用一個等式表示,這個等式叫做函數的解析表達式,簡稱解析式. 優點:一是簡明、全面地概括了變量間的關系;二是可以通過解析式求出任意一個自變量的值所對應的函數值.中學階段研究的函數主要是用解析法表示的函數. 2.列表法:就是列出表格來表示兩個變量的函數關系. 優點:不需要計算就可以直接看出與自變量的值相對應的函數值. 3.圖象法:就是用函數圖象表示兩個變量之間的關系. 優點:能直觀形象地表示出自變量的變化,相應的函數值變化的趨勢,這樣使得我們可以通過圖象來研究函數的某些性質. 點評:對于(1)可選用解析法和列表法.對于(2)通過函數的圖象來作比較比較簡捷.通過兩個問題的解答,歸納出表示函數的方法,常用的有解析法、列表法和圖象法三種.并讓學生體會到各種方法的優越性. |
|
通過解析式來求函數的值和數形結合的初步接觸. |


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源:設計必修一數學(人教A版) 人教A版 題型:044
17世紀,科學家們致力于運動的研究,如計算天體的位置,遠距離航海中對經度和緯度的測量,炮彈的速度對于高度和射程的影響等.諸如此類的問題都需要探究兩個變量之間的關系,并根據這種關系對事物的變化規律作出判斷,如根據炮彈的速度推測它能達到的高度和射程.這正是函數產生和發展的背景.

“function”一詞最初由德國數學家萊布尼茲(G.W.Leibniz,1646~1716)在1692年使用.在中國,清代數學家李善蘭(1811~1882)在1859年和英國傳教士偉烈亞力合譯的《代徽積拾級》中首次將“function”譯做“函數”.
萊布尼茲用“函數”表示隨曲線的變化而改變的幾何量,如坐標、切線等.1718年,他的學生,瑞士數學家約翰·伯努利(J.Bernoulli,1667~1748)強調函數要用公式表示.后來,數學家認為這不是判斷函數的標準.只要一些變量變化,另一些變量隨之變化就可以了.所以,1755年,瑞士數學家歐拉(L.Euler,1707~1783)將函數定義為“如果某些變量,以一種方式依賴于另一些變量,我們將前面的變量稱為后面變量的函數”.
當時很多數學家對于不用公式表示函數很不習慣,甚至抱懷疑態度.函數的概念仍然是比較模糊的.
隨著對微積分研究的深入,18世紀末19世紀初,人們對函數的認識向前推進了.德國數學家狄利克雷(P.G.L.Dirichlet,1805~1859)在1837年時提出:“如果對于x的每一個值,y總有一個完全確定的值與之對應,則y是x的函數”.這個定義較清楚地說明了函數的內涵.只要有一個法則,使得取值范圍中的每一個值,有一個確定的y和它對應就行了,不管這個法則是公式、圖象、表格還是其他形式.19世紀70年代以后,隨著集合概念的出現,函數概念又進而用更加嚴謹的集合和對應語言表述,這就是本節學習的函數概念.
綜上所述可知,函數概念的發展與生產、生活以及科學技術的實際需要緊密相關,而且隨著研究的深入,函數概念不斷得到嚴謹化、精確化的表達,這與我們學習函數的過程是一樣的.
你能以函數概念的發展為背景,談談從初中到高中學習函數概念的體會嗎?
1.探尋科學家發現問題的過程,對指導我們的學習有什么現實意義?
2.萊布尼茲、狄利克雷等科學家有哪些品質值得我們學習?
查看答案和解析>>
科目:高中數學 來源: 題型:044
平面直角坐標系內的向量都可以用一有序實數對唯一表示,這使我們想到可以用向量作為解析幾何的研究工具.如圖,設直線
l的傾斜角為α(α≠90°).在l上任取兩個不同的點 ,
, ,不妨設向量
,不妨設向量 的方向是向上的,那么向量
的方向是向上的,那么向量 的坐標是(
的坐標是( ).過原點作向量
).過原點作向量 ,則點P的坐標是(
,則點P的坐標是( ),而且直線OP的傾斜角也是α.根據正切函數的定義得
),而且直線OP的傾斜角也是α.根據正切函數的定義得
 ,
,
這就是《數學
2》中已經得到的斜率公式.上述推導過程比《數學2》中的推導簡捷.你能用向量作為工具討論一下直線的有關問題嗎?例如:(1)
過點 ,平行于向量
,平行于向量 的直線方程;
的直線方程;
(2)
向量(A,B)與直線 的關系;
的關系;
(3)
設直線 和
和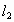 的方程分別是
的方程分別是
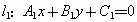

那么,
 ∥
∥ ,
, 的條件各是什么?如果它們相交,如何得到它們的夾角公式?
的條件各是什么?如果它們相交,如何得到它們的夾角公式?
(4)
點 到直線
到直線 的距離公式如何推導?
的距離公式如何推導?

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com