已知
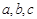
分別為△ABC三個內(nèi)角A、B、C的對邊,
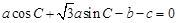
.
(1)求A;
(2)若
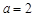
,△ABC 的面積為
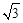
,求
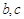
.
(1)

;(2)

.
試題分析:(1)由條件
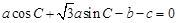
及正弦定理,進行邊角的統(tǒng)一,可得到

,注意到

,因此,可將等式繼續(xù)變形為

,從而得到

,由利用輔助角公式可變形為

,因此

,

;(2)由(1)及

面積為

,可得

,再根據(jù)余弦定理

,聯(lián)立方程即可解得

.
(1)由正弦定理及

可得:
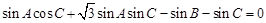
,
即

,
又∵

,∴

3分
即

,∴

,

; 7分
由(1)

及

,∴

,
又由余弦定理及

:

10分,
聯(lián)立方程,即可得

14分
練習冊系列答案
相關(guān)習題
科目:高中數(shù)學
來源:不詳
題型:解答題
(本小題滿分12分)已知函數(shù)
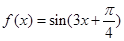
.
(1)求
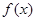
的單調(diào)遞增區(qū)間;
(2)若
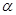
是第二象限角,
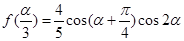
,求
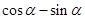
的值.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
為了得到函數(shù)
y=cos(2x-)的圖象,只需將函數(shù)y=cos2x的圖象( )
| A.向左平移個單位長度 | B.向右平移個單位長度 |
| C.向左平移個單位長度 | D.向右平移個單位長度 |
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
在

中,已知
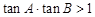
,則

是( )
| A.直角三角形 | B.鈍角三角形 |
| C.銳角三角形 | D.最小內(nèi)角大于45°的三角形 |
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
已知
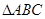
中,
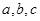
分別為
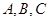
的對邊,
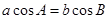
,則
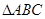
為( )
| A.等腰三角形 | B.直角三角形 |
| C.等腰直角三角形 | D.等腰或直角三角形 |
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
已知函數(shù)f(x)=6cos
2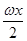
+
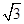
sinωx-3(ω>0)在一個周期內(nèi)的圖象如圖所示,A為圖象的最高點,B、C為圖象與x軸的交點,且△ABC為正三角形.
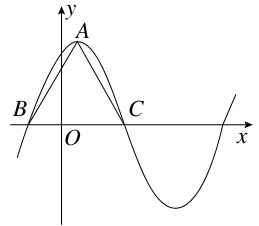
(1)求ω的值及函數(shù)f(x)的值域;
(2)若f(x
0)=
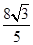
,且x
0∈(-
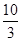
,
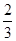
),求f(x
0+1)的值.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
若

為銳角,且sin

=

,則sin

的值為________.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
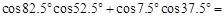
______________.
查看答案和解析>>

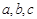 分別為△ABC三個內(nèi)角A、B、C的對邊,
分別為△ABC三個內(nèi)角A、B、C的對邊,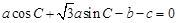 .
.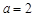 ,△ABC 的面積為
,△ABC 的面積為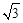 ,求
,求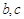 .
.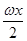 +
+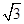 sinωx-3(ω>0)在一個周期內(nèi)的圖象如圖所示,A為圖象的最高點,B、C為圖象與x軸的交點,且△ABC為正三角形.
sinωx-3(ω>0)在一個周期內(nèi)的圖象如圖所示,A為圖象的最高點,B、C為圖象與x軸的交點,且△ABC為正三角形.
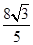 ,且x0∈(-
,且x0∈(-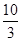 ,
,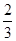 ),求f(x0+1)的值.
),求f(x0+1)的值.