
函數 是定義在R上的奇函數,當
是定義在R上的奇函數,當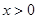 時,
時,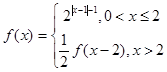 ,則
,則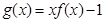 在
在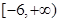 上所有零點之和為 .
上所有零點之和為 .
8
解析試題分析:∵函數f(x)是定義在R上的奇函數,∴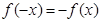 ,又∵函數
,又∵函數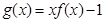 ,∴
,∴ ∴函數g(x)是偶函數,∴函數
∴函數g(x)是偶函數,∴函數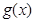 的零點都是以相反數的形式成對出現的.∴函數
的零點都是以相反數的形式成對出現的.∴函數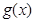 在[-6,6]上所有的零點的和為0,∴函數
在[-6,6]上所有的零點的和為0,∴函數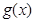 在[-6,+∞)上所有的零點的和,即函數
在[-6,+∞)上所有的零點的和,即函數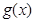 在(6,+∞)上所有的零點之和.由0<x≤2時,
在(6,+∞)上所有的零點之和.由0<x≤2時,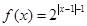 ,即
,即 ∴函數
∴函數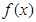 在(0,2]上的值域為
在(0,2]上的值域為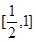 ,當且僅當x=2時,
,當且僅當x=2時,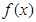 =1;
=1;
又∵當x>2時,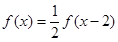
∴函數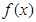 在(2,4]上的值域為
在(2,4]上的值域為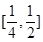 ,當且僅當x=4時,
,當且僅當x=4時,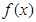 =
=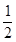 ;
;
函數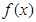 在(4,6]上的值域為
在(4,6]上的值域為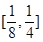 ,當且僅當x=6時,
,當且僅當x=6時,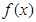 =
=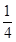 ;
;
函數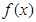 在(6,8]上的值域為
在(6,8]上的值域為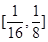 ,當且僅當x=8時,
,當且僅當x=8時,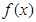 =
= ;
;
函數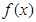 在(8,10]上的值域為
在(8,10]上的值域為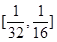 ,當且僅當x=10時,
,當且僅當x=10時,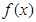 =
=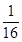 ;
;
故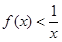 在(8,10]上恒成立,
在(8,10]上恒成立,
注意到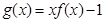 的零點就是函數
的零點就是函數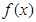 的圖象與曲線
的圖象與曲線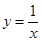 交點的橫坐標,
交點的橫坐標,
所以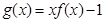 在(8,10]上無零點;
在(8,10]上無零點;
同理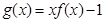 在(10,12]上無零點;
在(10,12]上無零點;
依此類推,函數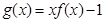 在(8,+∞)無零點;
在(8,+∞)無零點;
綜上函數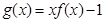 在[-6,+∞)上的所有零點之和為8;故應填入:8.
在[-6,+∞)上的所有零點之和為8;故應填入:8.
如下圖:
考點:1.奇偶性與單調性的綜合;2.函數的零點.


湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com