已知函數f(x)=x2+3x,數列{an}的前n項和為Sn,且對一切正整數n,點Pn(n,Sn)都在函數f(x)的圖象上.
(1)求數列{an}的通項公式;
(2)設A={x|x=an,n∈N*},B={x|x=2(an-1),n∈N*},等差數列{bn}的任一項bn∈A∩B,其中b1是A∩B中最的小數,且88<b8<93,求{bn}的通項公式;
(3)設數列{cn}滿足cn+2-cn=a1,且c1=c,c2=a2-c,若數列{cn}為單調遞增數列,求實數c的取值范圍.
解:(1)∵點P
n(n,S
n)都在函數f(x)=x
2+3x的圖象上,∴
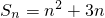
.
當n≥2時,
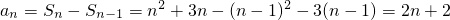
,
當n=1時,a
1=S
1=4,也滿足上式.
故a
n=2n+2.
(2)∵A={x|x=2n+2,n∈N
*},B={x|x=4n+2,n∈N
*},∴A∩B=B,
又∵b
n∈A∩B,∴b
n∈B即數列{b
n}的公差是4 的倍數
又A∩B中的最小數為6,∴b
1=6,∴b
8=4k+6,k∈N
*,
又∵88<b
8<93
∴
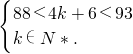
,解得k=21.
設等差數列{b
n}的公差為d,由b
8=6+7d=90得d=12
故b
n=12n-6
(3)由a
n=2n+2知c
n+2-c
n=4,即數列{c
2k-1}和{c
2k}分別是以c
1=c,c
2=6-c為首項,4為公差的等差數列
所以c
2k-1=c+4k-4,c
2k=c
2+4(k-1)=4k-c+2,c
2k+1=4k+c
∵數列{c
n}是單調遞增數列,∴c
2k-1<c
2k<c
2k+1對任意的k∈N
*成立.
∴
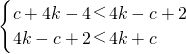
,解得1<c<3
∴實數c的取值范圍是1<c<3
分析:(1)根據點P
n(n,S
n)都在函數f(x)=x
2+3x的圖象上,可得
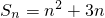
,再寫一式,兩式相減,結合n=1時,a
1=S
1=4,即可求得數列{a
n}的通項公式;
(2)先確定數列{b
n}的公差是4 的倍數,根據A∩B中的最小數為6,可得b
8=4k+6,利用88<b
8<93,可得k的值,進而可求等差數列{b
n}的公差,從而可得{b
n}的通項公式;
(3)由a
n=2n+2知c
n+2-c
n=4,即數列{c
2k-1}和{c
2k}分別是以c
1=c,c
2=6-c為首項,4為公差的等差數列,利用數列{c
n}是單調遞增數列,建立不等式,即可求得實數c的取值范圍.
點評:本題考查數列與函數的關系,考查數列的通項,考查數列的單調性,考查學生分析解決問題的能力,屬于中檔題.

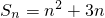 .
.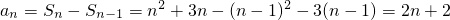 ,
,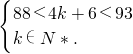 ,解得k=21.
,解得k=21. 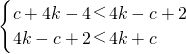 ,解得1<c<3
,解得1<c<3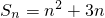 ,再寫一式,兩式相減,結合n=1時,a1=S1=4,即可求得數列{an}的通項公式;
,再寫一式,兩式相減,結合n=1時,a1=S1=4,即可求得數列{an}的通項公式; 

 已知函數f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函數f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<