Question

斜率為-2的橢圓x²+2y²=2的動弦中點軌跡方程是．

Answer 1

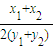
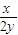
【答案】分析：設出直線的方程，直線與橢圓的交點，直線方程代入橢圓方程，兩式相減可求得k=-2=，設出中點的坐標，進而可求得-2=，則點p的軌跡可求得．
解答：解：設直線方程為：y=-2x+m；
設直線與橢圓交點分別為A，B，設A（x₁，y₁） B（x₂，y₂）
又因為x₁²+2y₁²=2       （1）
x₂²+2y₂²=2             （2）
（1）-（2）得：x₁²-x₂²=2y₂²-2y₁²
（x₁+x₂）（x₁-x₂）=-2（y₁+y₂）（y₁-y₂）
k=-2=-
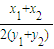
設中點為P（x，y）
所以2=
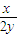
x-4y=0
點評：本題主要考查了直線與圓錐曲線的綜合問題．涉及弦的中點及中點弦問題，利用差分法較為簡便．