【答案】
分析:(1)根據對數函數定義可知定義域為大于0的數,求出f′(x)討論當a-1=1時導函數大于0,函數單調遞增;當a-1<1時分類討論函數的增減性;當a-1>1時討論函數的增減性.
(2)構造函數g(x)=f(x)+x,求出導函數,根據a的取值范圍得到導函數一定大于0,則g(x)為單調遞增函數,則利用當x
1>x
2>0時有g(x
1)-g(x
2)>0即可得證.
解答:解:(1)f(x)的定義域為(0,+∞).
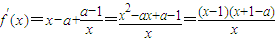
(i)若a-1=1即a=2,則

故f(x)在(0,+∞)單調增.
(ii)若a-1<1,而a>1,
故1<a<2,則當x∈(a-1,1)時,f′(x)<0;
當x∈(0,a-1)及x∈(1,+∞)時,f′(x)>0
故f(x)在(a-1,1)單調減,
在(0,a-1),(1,+∞)單調增.
(iii)若a-1>1,即a>2,
同理可得f(x)在(1,a-1)單調減,
在(0,1),(a-1,+∞)單調增.
(2)考慮函數g(x)=f(x)+x=

則
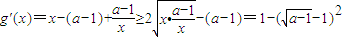
由于1<a<5,故g'(x)>0,
即g(x)在(0,+∞)單調增加,
從而當x
1>x
2>0時有g(x
1)-g(x
2)>0,
即f(x
1)-f(x
2)+x
1-x
2>0,故
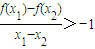
,
當0<x
1<x
2時,有
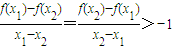 點評:
點評:考查學生利用導數研究函數單調性的能力,以及基本不等式證明的能力.

 x2-ax+(a-1)lnx,a>1.
x2-ax+(a-1)lnx,a>1.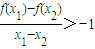 .
.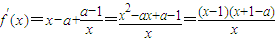


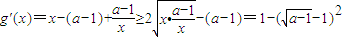
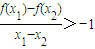 ,
,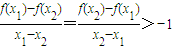


 輕松課堂單元測試AB卷系列答案
輕松課堂單元測試AB卷系列答案 小題狂做系列答案
小題狂做系列答案 已知函數f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函數f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<