
數列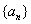 中,
中, ,
,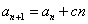 (
(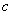 是常數,
是常數,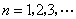 ),且
),且 成公比不為
成公比不為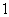 的等比數列,則
的等比數列,則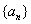 的通項公式是 .
的通項公式是 .
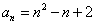
【解析】
試題分析:a1=2,a2=2+c,a3=2+3c,因為a1,a2,a3成等比數列,所以(2+c)2=2(2+3c),解得c=0或c=2.當c=0時,a1=a2=a3,不符合題意舍去,故c=2.當n≥2時,由于a2-a1=c,a3-a2=2c,an-an-1=(n-1)c,所以an-a1=[1+2++(n-1)]c=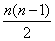 c.又a1=2,c=2,故an=2+n(n-1)=n2-n+2(n=2,3,).當n=1時,上式也成立,所以an=n2-n+2
c.又a1=2,c=2,故an=2+n(n-1)=n2-n+2(n=2,3,).當n=1時,上式也成立,所以an=n2-n+2
考點:本題考查了數列的性質和應用
點評:掌握常見數列通項公式的求法如疊加法、疊乘法是解決此類問題的關鍵,解題時要注意計算能力的培養.


 A加金題 系列答案
A加金題 系列答案 全優測試卷系列答案
全優測試卷系列答案科目:高中數學 來源:2007年普通高等學校招生全國統一考試理科數學卷(北京) 題型:解答題
(本小題共13分)數列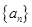 中,
中,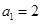 ,
,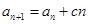 (
(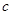 是常數,
是常數,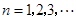 ),且
),且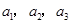 成公比不為
成公比不為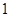 的等比數列.
的等比數列.
(I)求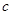 的值;
的值;
(II)求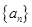 的通項公式.
的通項公式.
查看答案和解析>>
科目:高中數學 來源:2012-2013學年陜西省高三第七次適應性訓練文科數學試卷(解析版) 題型:解答題
數列 中,
中,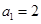 ,
,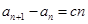 (
(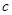 是常數,
是常數,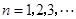 ),且
),且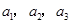 成公比不為
成公比不為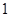 的等比數列.
的等比數列.
(Ⅰ)求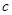 的值;
的值;
(Ⅱ)求 的通項公式.
的通項公式.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com