Question

11．已知函數f（x）=2sin （2x+$\frac{π}{6}$）．
（1）求函數f（x）的最小正周期及其單調減區間；
（2）用“五點法”畫出函數g（x）=f（x），x∈[-$\frac{7π}{12}$，$\frac{5π}{12}$]的圖象（完成列表格并作圖），由圖象研究并寫出g（x）的對稱軸和對稱中心．

Answer 1

分析 （1）根據正弦函數的圖象與性質，求出f（x）的最小正周期與單調減區間；
（2）根據題意列出表格，根據表格畫出函數在x∈[-$\frac{7π}{12}$，$\frac{5π}{12}$]的圖象，
結合圖象得出此函數沒有對稱軸，有一個對稱中心．

解答 解：（1）函數f（x）=2sin （2x+$\frac{π}{6}$），
∴f（x）的最小正周期為T=$\frac{2π}{2}$=π；
令2kπ+$\frac{π}{2}$≤2x+$\frac{π}{6}$≤2kπ+$\frac{3π}{2}$，k∈Z，
則2kπ+$\frac{π}{3}$≤2x≤2kπ+$\frac{4π}{3}$，k∈Z，
kπ+$\frac{π}{6}$≤x≤kπ+$\frac{2π}{3}$，k∈Z；
∴函數f（x）的單調減區間為[kπ+$\frac{π}{6}$，kπ+$\frac{2π}{3}$]（k∈Z）；
（2）根據題意列出表格得：

x	-$\frac{7π}{12}$	-$\frac{π}{3}$	-$\frac{π}{12}$	$\frac{π}{6}$	$\frac{5π}{12}$
2x+$\frac{π}{6}$	-π	-$\frac{π}{2}$	0	$\frac{π}{2}$	π
y=2sin（2x+$\frac{π}{6}$）	0	-2	0	2	0

根據表格畫出函數g（x）=f（x），x∈[-$\frac{7π}{12}$，$\frac{5π}{12}$]的圖象如圖所示，

從圖象上可以直觀看出，此函數沒有對稱軸，有一個對稱中心，對稱中心是（-$\frac{π}{12}$，0）．

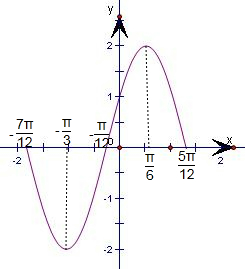
點評 本題考查了正弦函數的周期性和單調性以及五點法做正弦函數的圖象問題，是基礎題目．