
已知:直線a∥直線b,a⊥平面α,
求證:b⊥α.
證法一:如下圖,在α內(nèi)任取一條直線g.
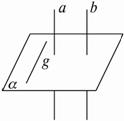
∵a⊥α,g![]() α,∴a⊥g.
α,∴a⊥g.
∵a∥b,∴b⊥g.
由直線和平面垂直的定義知b⊥α.
證法二:如下圖設m、n是α內(nèi)的兩條相交直線.
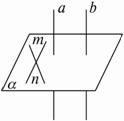
∵a⊥α,m、n![]() α,∴a⊥m,a⊥n.
α,∴a⊥m,a⊥n.
∵a∥b,∴b⊥m,b⊥n.
由直線和平面垂直的判定定理知b⊥α.
證法三:如下圖,假設b和α不垂直,則在α內(nèi)至少有一條直線c和b不垂直.
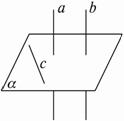
∵a⊥α,∴a⊥c.
∵a∥b,∴b⊥C.
這與b和C不垂直矛盾.
∴b⊥α.
點評:利用定義證明直線和平面垂直時,需在平面內(nèi)任取一條直線;利用判定定理證明直線和平面垂直時,需在平面內(nèi)取兩條相交直線.證直線和平面垂直,最后都轉(zhuǎn)化成了證直線和直線垂直.本例的結(jié)論也是判定直線和平面垂直的一種方法.


 名校提分一卷通系列答案
名校提分一卷通系列答案 課程達標測試卷闖關100分系列答案
課程達標測試卷闖關100分系列答案 新卷王期末沖刺100分系列答案
新卷王期末沖刺100分系列答案 全能闖關100分系列答案
全能闖關100分系列答案科目:高中數(shù)學 來源: 題型:
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
查看答案和解析>>
科目:高中數(shù)學 來源:2013-2014學年陜西咸陽范公中學高三上學期摸底考試文科數(shù)學試卷(解析版) 題型:選擇題
下列命題中正確的個數(shù)是( ).
(1)若直線 上有無數(shù)個點不在平面
上有無數(shù)個點不在平面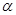 內(nèi),則
內(nèi),則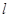 ∥
∥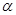 .
.
(2)若直線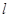 與平面
與平面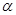 平行,則
平行,則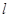 與平面
與平面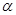 內(nèi)的任意一條直線都平行.
內(nèi)的任意一條直線都平行.
(3)如果兩條平行直線中的一條與一個平面平行,那么另一條也與這個平面平行.
(4)若直線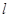 與平面
與平面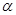 平行,則
平行,則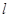 與平面
與平面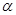 內(nèi)的任意一條直線都沒有公共點.
內(nèi)的任意一條直線都沒有公共點.
A.0 B. 1 C. 2 D.3
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com