
分析 由已知求出$\overrightarrow{a}•\overrightarrow{b}$的值,然后展開數量積得答案.
解答 解:∵|$\overrightarrow{a}$|=2,|$\overrightarrow{b}$|=3,$\overrightarrow{a}$與$\overrightarrow{b}$的夾角為$\frac{2π}{3}$,
∴$\overrightarrow{a}•\overrightarrow{b}=|\overrightarrow{a}||\overrightarrow{b}|cos\frac{2π}{3}=2×3×(-\frac{1}{2})=-3$.
∴($\overrightarrow{a}$-2$\overrightarrow{b}$)•(2$\overrightarrow{a}$+$\overrightarrow{b}$)=$2{\overrightarrow{a}}^{2}-3\overrightarrow{a}•\overrightarrow{b}-2{\overrightarrow{b}}^{2}$=2×4-3×(-3)-2×9=-1.
故答案為:-1.
點評 本題考查平面向量的數量積運算,是基礎的計算題.


科目:高中數學 來源: 題型:解答題
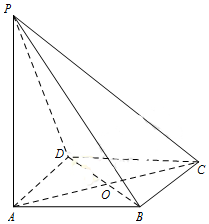 如圖,ABCD是菱形,PA⊥平面ABCD,PA=AD=2,∠BAD=60°.
如圖,ABCD是菱形,PA⊥平面ABCD,PA=AD=2,∠BAD=60°.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | [$\sqrt{3}$-1,$\sqrt{3}$+1] | B. | [1,3] | C. | [$\sqrt{3}$-1,2] | D. | [1,$\sqrt{3}$+1] |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | |a|<|b| | B. | $\frac{1}{a}>\frac{1}{b}$ | C. | ${(\frac{1}{2})^a}>{(\frac{1}{2})^b}$ | D. | lna>lnb |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\sqrt{3}-1$ | B. | $\sqrt{3}+1$ | C. | $\frac{{\sqrt{3}+1}}{2}$ | D. | $\sqrt{3}+1$或$\frac{{\sqrt{3}+1}}{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $(2k-\frac{1}{4},2k+\frac{1}{4}),k∈Z$ | B. | $(2k+\frac{1}{2},2k+\frac{5}{2}),k∈Z$ | ||
| C. | $(4k-\frac{1}{4},4k+\frac{1}{4}),k∈Z$ | D. | $(4k+\frac{1}{4},4k+\frac{15}{4}),k∈Z$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com