設直線y=kx+1與圓C:x2+y2-2kx-2my-7=0交于M,N兩點,且M,N關于直線x+y=0對稱,
(Ⅰ)求m,k的值;
(Ⅱ)若直線x=ay+1與C交P,Q兩點,是否存在實數a使得OP⊥OQ,如果存在,求出a的值;如果不存在,請說明理由.
解:(Ⅰ)由M,N關于直線x+y=0對稱,可知所求的直線的斜率k=1
∵根據圓的性質可得直線y+x=0過圓的圓心C(1,m)
∴m=-1
(Ⅱ)把x=ay+1代入(x-1)
2+(y+1)
2=9得(1+a
2)y
2+2y-8=0
設P(x
1,y
1),Q(x
2,y
2),則
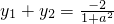
,
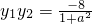
若OP⊥OQ,則有x
1x
2+y
1y
2=(ay
1+1)(ay
2+1)+y
1y
2=(1+a
2)y
1y
2+a(y
1+y
2)+1=
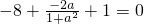
即7a
2+2a+7=0,方程無實數根,所以滿足條件的實數a不存在.
分析:(Ⅰ)由M,N關于直線x+y=0對稱,可知所求的直線的斜率k=1,根據圓的性質可得直線y+x=0過圓的圓心C(1,m)代入可求m
(Ⅱ)把x=ay+1代入(x-1)
2+(y+1)
2=9得(1+a
2)y
2+2y-8=0,設P(x
1,y
1),Q(x
2,y
2),則
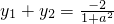
,
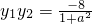
,若OP⊥OQ,則有x
1x
2+y
1y
2=0,代入整理可求
點評:本題主要考查了直線與圓的方程的性質的應用,解(I)的關鍵是根據圓的性質可得直線x+y=0過圓心的條件,而
(II)是直線與圓的一般類型的試題,體現了方程的思想的應用.

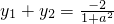 ,
,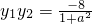
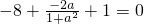
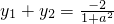 ,
,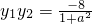 ,若OP⊥OQ,則有x1x2+y1y2=0,代入整理可求
,若OP⊥OQ,則有x1x2+y1y2=0,代入整理可求

 閱讀快車系列答案
閱讀快車系列答案