
(本題滿分12分)為了了解某年段1000名學生的百米成績情況,隨機抽取了若
干學生的百米成績,成績全部介于13秒與18秒之間,將成績按如下方式分成五組:第一組
[13,14);第二組[14,15);……;第五組[17,18].按上述分組方法得到的頻率分布直方圖如
圖所示,已知圖中從左到右的前3個組的頻率之比為3∶8∶19,且第二組的頻數為8.
(1)將頻率當作概率,請估計該年段學生中百米成績在[16,17)內的人數;
(2)求調查中隨機抽取了多少個學生的百米成績;
(3)若從第一、五組中隨機取出兩個成績,求這兩個成績的差的絕對值大于1秒的概率.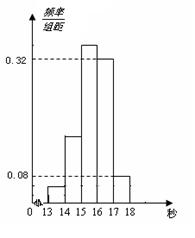
解:(1)百米成績在[16,17)內的頻率為0.32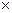 1="0.32." 0.32
1="0.32." 0.32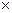 1000=320
1000=320
∴估計該年段學生中百米成績在[16,17)內的人數為320人。 ……2分
(2)設圖中從左到右前3個組的頻率分別為3x,8x ,19x 依題意,得
3x+8x+19x+0.32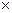 1+0.08
1+0.08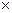 1="1" ,∴x="0.02 " ……4分
1="1" ,∴x="0.02 " ……4分
設調查中隨機抽取了n 個學生的百米成績,則 ∴n=50
∴n=50
∴調查中隨機抽取了50個學生的百米成績. ……6分
(3)百米成績在第一組的學生數有3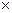 0.02
0.02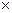 1
1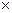 50=3,記他們的成績為a,b,c百米成績在第五組的學生數有0.08
50=3,記他們的成績為a,b,c百米成績在第五組的學生數有0.08 1
1 50= 4,記他們的成績為m,n,p,q則從第一、五組中隨機取出兩個成績包含的基本事件有{a,b},{a,c},{a,m},{a,n},{a,p},{a,q},{b,c},{b,m},{b,n},{b,p},{b,q},{c,m},{c,n},{c,p},{c,q},{m,n},{m,p},{m,q},{n,p},{n,q},{p,q},共21個 ……9分
50= 4,記他們的成績為m,n,p,q則從第一、五組中隨機取出兩個成績包含的基本事件有{a,b},{a,c},{a,m},{a,n},{a,p},{a,q},{b,c},{b,m},{b,n},{b,p},{b,q},{c,m},{c,n},{c,p},{c,q},{m,n},{m,p},{m,q},{n,p},{n,q},{p,q},共21個 ……9分
其中滿足成績的差的絕對值大于1秒所包含的基本事件有{a,m},{a,n},{a,p},{a,q},{b,m},{b,n},{b,p},{b,q},{c,m},{c,n},{c,p},{c,q},共12個,……10分
所以P= ……12分
……12分
解析


科目:高中數學 來源: 題型:解答題
(本題滿分12分)某電視臺在一次對收看文藝節目和新聞節目觀眾的抽樣調查中,隨機抽取了100名電視觀眾,相關的數據如下表所示:
| | 文藝節目 | 新聞節目 | 總計 |
| 20至40歲 | 40 | 10 | 50 |
| 大于40歲 | 20 | 30 | 50 |
| 總計 | 60 | 40 | 100 |
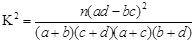
| P(k2>k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.84 | 5.024 | 6.635 | 7.879 | 10.83 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
為抗擊金融風暴,某系統決定對所屬企業給予低息貸款的扶持,該系統制定了評分標準,并根據標準對企業進行評估,然后依據評估得分將這些企業分別定為優秀、良好、合格、不合格四個等級,并根據等級分配相應的低息貸款數額,為了更好地掌握貸款總額,該系統隨機抽查了所屬的部分企業.一下圖表給出了有關數據(將頻率看做概率)
(1)任抽一家所屬企業,求抽到的企業等級是優秀或良好的概率;
(2)對照標準,企業進行了整改.整改后,如果優秀企業數量不變,不合格企業、合格企業、良好企業的數量成等差數列.要使所屬企業獲得貸款的平均值(即數學期望)不低于410萬元,那么整改后不合格企業占企業總數百分比的最大值是多少?

查看答案和解析>>
科目:高中數學 來源: 題型:解答題
在學校開展的綜合實踐活動中,某班進行了小制作評比,作品上交時間為5 月1日至30日,評委會把同學們上交作品的件數按5天一組分組統計,繪制了頻率分布直方圖(如圖),已知從左到右各長方形的高的比為2:3:4:6:4:1,第三組的頻數為12,請回答下列問題:
(1)本次活動共有多少件作品參加評比?
(2)經過評比,第四組和第六組分別有10件和2件 作品獲獎,問這兩組哪組獲獎率更高?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(12分)(理)在某校舉行的數學競賽中,全體參賽學生的競賽成績近似服從正態分布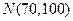 。已知成績在90分以上(含90分)的學生有12名。
。已知成績在90分以上(含90分)的學生有12名。
(Ⅰ)、試問此次參賽學生總數約為多少人?
(Ⅱ)、若該校計劃獎勵競賽成績排在前50名的學生,試問設獎的分數線約為多少分?可共查閱的(部分)標準正態分布表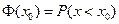
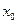 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 1.2 1.3 1.4 1.9 2.0 2.1 | 0.8849 0.9032 0.9192 0.9713 0.9772 0.9821 | 0.8869 0.9049 0.9207 0.9719 0.9778 0.9826 | 0.888 0.9066 0.9222 0.9726 0.9783 0.9830 | 0.8907 0.9082 0.9236 0.9732 0.9788 0.9834 | 0.8925 0.9099 0.9251 0.9738 0.9793 0.9838 | 0.8944 0.9115 0.9265 0.9744 0.9798 0.9842 | 0.8962 0.9131 0.9278 0.9750 0.9803 0.9846 | 0.8980 0.9147 0.9292 0.9756 0.9808 0.9850 | 0.8997 0.9162 0.9306 0.9762 0.9812 0.9854 | 0.9015 0.9177 0.9319 0.9767 0.9817 0.9857 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題滿分12分) 某種產品的廣告費用支出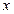 (萬元)與銷售額y(萬元)之間有如下的對應數據
(萬元)與銷售額y(萬元)之間有如下的對應數據
(1)求回歸直線方程;
(2)據此估計廣告費用為10銷售收入 的值
的值
(參考 公式:
公式: 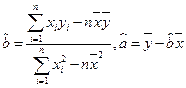 )
)
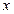 |  2 2 | 4 | 5 | 6 | 8 |
 | 30 | 40 | 60 | 50 | 70 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題滿分13分)
某種產品的廣告費支出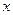 與銷售額
與銷售額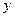 (單位:萬元)之間有如下對應數據:
(單位:萬元)之間有如下對應數據:
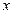 | 2 | 4 | 5 | 6 | 8 |
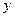 | 30 | 40 | 60 | 50 | 70 |
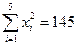
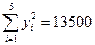
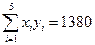 ,
,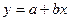 ,其中
,其中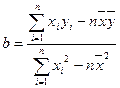 )
)查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某工廠2010年第三季度生產的A,B,C,D四種型號的產品產量用條形圖形表示如圖,現用分層抽樣的方法從中選取50件樣品參加2011年4月份的一個展銷會。
(1)A,B,C,D型號的產品各抽取多少件?
(2)從50件樣品隨機地抽取2件,求這2件產品恰好是不同型號產品的概率。
(3)從A,C型號的樣品中隨機地抽取3件,用ξ表示抽取A型號的產品件數,求ξ的分布列和數學期望
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某校組織一次籃球投籃測試,已知甲同學每次投籃的命中率均為1/2。
(1)若規定每投進1球得2分,甲同學投籃4次,求總得分X的概率分布和數學期望。
(2)假設連續3次投籃未中或累計7次投籃未中,則停止投籃測試,問:甲同學恰好投籃10次,被停 止投籃測試的概率是多少?
止投籃測試的概率是多少?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com