已知函數(shù)
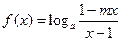
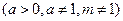
是奇函數(shù).
(1)求實數(shù)
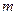
的值;
(2)判斷函數(shù)
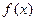
在
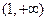
上的單調(diào)性,并給出證明;
(3)當(dāng)
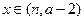
時,函數(shù)
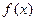
的值域是
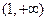
,求實數(shù)
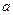
與
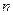
的值
1解:(1)由已知條件得

對定義域中的

均成立.………………………………1分


即



對定義域中的

均成立.


即

(舍去)或

. …………………………………4分
(2)由(1)得

設(shè)

,

當(dāng)

時,



. ………………………………6分
當(dāng)

時,

,即

.

當(dāng)

時,
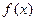
在
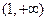
上是減函數(shù). …

…………

…………………8分
同理當(dāng)

時,
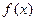
在
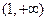
上是增函數(shù). ………………………10分
(3)

函數(shù)
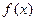
的定義域為

,

①

,


.

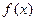
在

為增函數(shù),
要使值域為
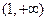
,
則

(無解)
②

,


.

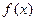
在

為減函數(shù),
要使
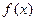
的值域為
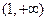
, 則



,

. ……………………………14分
練習(xí)冊系列答案
相關(guān)習(xí)題
科目:高中數(shù)學(xué)
來源:不詳
題型:單選題
若函數(shù)
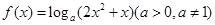
在區(qū)間
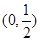
內(nèi)恒有
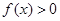
,則
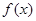
的單調(diào)遞增區(qū)間為( )
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
已知函數(shù)

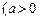
且
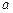
≠1)
(1)求此函數(shù)的定義域;
(2)討論
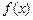
的單調(diào)性。(12分)

查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
已知

(

)=

,
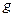
(

)=

且

.
(Ⅰ)當(dāng)

=4,

∈(0,+

),且F(

)=
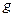
(

)-

(

)有最小值2時,求

的值;
(Ⅱ)當(dāng)0



1,

∈(0,+

)時,有

(

)≥
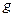
(

)恒成立,求實數(shù)

的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:單選題
若函數(shù)
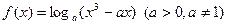
在區(qū)間
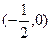
內(nèi)單調(diào)遞增,則a的
取值范圍是( )
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:單選題
若
a>0,且
a≠1,且
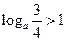
,則實數(shù)
a的取值范圍是
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:單選題
若f(x)=|lgx|,當(dāng)a<b<c時,f(a)>f(c)>f(b).則下列不等式中正確的為( )。
| A.(a-1)(c-1)>0 | B.a(chǎn)c>1 | C.a(chǎn)c=1 | D.a(chǎn)c<1 |
查看答案和解析>>

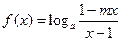
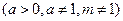 是奇函數(shù).
是奇函數(shù).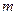 的值;
的值;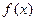 在
在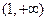 上的單調(diào)性,并給出證明;
上的單調(diào)性,并給出證明;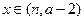 時,函數(shù)
時,函數(shù)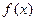 的值域是
的值域是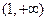 ,求實數(shù)
,求實數(shù)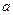 與
與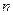 的值
的值 名校課堂系列答案
名校課堂系列答案 (
( )=
)= ,
,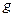 (
( )=
)= 且
且 .
. =4,
=4, ∈(0,+
∈(0,+ ),且F(
),且F( )=
)=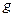 (
( )-
)- (
( )有最小值2時,求
)有最小值2時,求 的值;
的值;

 1,
1, ∈(0,+
∈(0,+ )時,有
)時,有 (
( )≥
)≥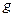 (
( )恒成立,求實數(shù)
)恒成立,求實數(shù) 的取值范圍.
的取值范圍.