Question

已知點F₁（-4，0），F₂（4，0），又P（x，y）是曲線上的點，則（ ）
A．|PF₁|+|PF₂|=10
B．|PF₁|+|PF₂|＜10
C．|PF₁|+|PF₂|≤10
D．|PF₁|+|PF₂|≥10

Answer 1

【答案】分析：法一：根據方程，可以聯想橢圓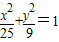，根據橢圓的定義可知，是以點F₁（-4.0），F₂（4，0）為焦點的橢圓，在橢圓上任意取點，可以證明點在曲線的內部或在曲線上，即橢圓上的點在封閉曲線的內部或曲線上，故可得結論．
法二：任取點P（x，y）在曲線上，可令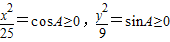，A∈[0，]，易證得sinA+cosA≥1，即由此知點P（x，y）在上可其外部，再由橢圓的定義易選出正確選項
解答：解：根據方程，可以聯想橢圓，
在橢圓上取點Q（5cosα，3sinα），即x=5cosα，y=3sinα
則=2
∵0≤sin²α≤1，
∴
即點Q在曲線的內部或在曲線上
所以橢圓上的點在封閉曲線的內部或曲線上
由題意，是以點F₁（-4.0），F₂（4，0）為焦點的橢圓
∴當P點恰好取在頂點上時，此時點P在橢圓上，故有|PF₁|+|PF₂|=10
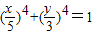點P不在曲線的頂點上時，必有點P在橢圓的外部，故|PF₁|+|PF₂|＞10
綜上所述，|PF₁|+|PF₂|≥10
故選D．
法二：任取點P（x，y）在曲線上，可令，A∈[0，]
則有sinA+cosA≥1，即由此知點P（x，y）在上可其外部，故有|PF₁|+|PF₂|≥10
故選D
點評：本題以曲線為載體，考查類比思想，考查橢圓的定義，考查學生分析解決問題的能力．