
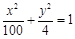 �����c(di��n)F���A
�����c(di��n)F���A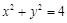 ���о�FT���E�A���c(di��n)P�����c(di��n)Tλ��F��P֮�g��M�龀��FP�����c(di��n)��Mλ��F��T֮�g���t
���о�FT���E�A���c(di��n)P�����c(di��n)Tλ��F��P֮�g��M�龀��FP�����c(di��n)��Mλ��F��T֮�g���t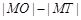 ��ֵ��_____________
��ֵ��_____________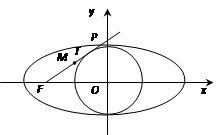
 �_���ܠ�Ԫ���I(y��)ϵ�д�
�_���ܠ�Ԫ���I(y��)ϵ�д� �n�r(sh��)�ƿ��S�þ���(x��)ϵ�д�
�n�r(sh��)�ƿ��S�þ���(x��)ϵ�д� һ�nһ��һ��ͨϵ�д�
һ�nһ��һ��ͨϵ�д�
| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ����Ԕ �}�ͣ�����}
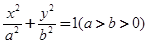 ���x����
���x����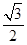 ���ҽ��c(di��n)��ֱ��
���ҽ��c(di��n)��ֱ��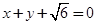 �ľ��x��
�ľ��x��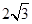 ���^(gu��)
���^(gu��)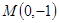 ��ֱ��
��ֱ��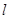 ���E�A��
���E�A��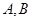 ���c(di��n).(��) ��E�A�ķ��̣����� ��ֱ��
���c(di��n).(��) ��E�A�ķ��̣����� ��ֱ��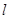 ��
��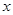 �S��
�S��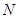 ,
,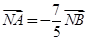 ,��ֱ��
,��ֱ��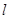 �ķ���.
�ķ���.�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ����Ԕ �}�ͣ�����}
 �ϵ��c(di��n)���ҽ��c(di��n)F����С���x��
�ϵ��c(di��n)���ҽ��c(di��n)F����С���x�� ��
�� ������c(di��n)�ľ��x��
������c(di��n)�ľ��x��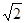 ���c(di��n)
���c(di��n) �Ǿ���
�Ǿ��� �ϵ�һ��(g��)��(d��ng)�c(di��n).
�ϵ�һ��(g��)��(d��ng)�c(di��n). ���c
���c �S����ֱ��ֱ��
�S����ֱ��ֱ�� �c�E�A����
�c�E�A���� ��
�� ���c(di��n),ʹ��
���c(di��n),ʹ�� ,���f(shu��)������.
,���f(shu��)������.�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ����Ԕ �}�ͣ�����}
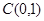 �ęE�A
�ęE�A ��
��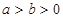 �����x���ʞ�
�����x���ʞ� ���E�A�c
���E�A�c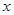 �S�Ľ��ڃ��c(di��n)
�S�Ľ��ڃ��c(di��n)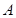 ��
��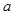 ��
��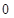 ����
����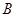 ��
�� ��
��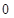 ��,�^(gu��)�c(di��n)
��,�^(gu��)�c(di��n)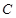 ��ֱ��
��ֱ��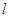 �c�E�A������һ�c(di��n)
�c�E�A������һ�c(di��n)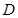 �����c
�����c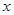 �S�����c(di��n)
�S�����c(di��n)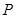 ��ֱ��
��ֱ��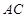 �cֱ��
�cֱ�� ���c�c(di��n)
���c�c(di��n)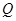 ��
��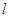 �^(gu��)�E�A�ҽ��c(di��n)�r(sh��)����
�^(gu��)�E�A�ҽ��c(di��n)�r(sh��)����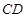 ���L(zh��ng)��
���L(zh��ng)��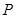 ����
���� ���c(di��n)�r(sh��)�����C��
���c(di��n)�r(sh��)�����C��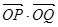 �鶨ֵ��
�鶨ֵ��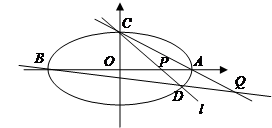
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ����Ԕ �}�ͣ�����}
 �����ҽ��c(di��n)�քe��
�����ҽ��c(di��n)�քe�� ���c(di��n)
���c(di��n) �ڙE�A�ϣ���(d��ng)
�ڙE�A�ϣ���(d��ng) �r(sh��)��
�r(sh��)�� ����e�� .
����e�� . �鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ����Ԕ �}�ͣ�����}
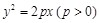 �Ľ��c(di��n)Fǡ���ǙE�A
�Ľ��c(di��n)Fǡ���ǙE�A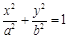 ���ҽ��c(di��n)���҃ɗl�������c(di��n)���B���^(gu��)�c(di��n)F���tԓ�E�A���x���ʞ�____________��
���ҽ��c(di��n)���҃ɗl�������c(di��n)���B���^(gu��)�c(di��n)F���tԓ�E�A���x���ʞ�____________���鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ����Ԕ �}�ͣ����x�}
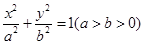 �c�p����
�c�p���� �й�ͬ�Ľ��c(di��n)��
�й�ͬ�Ľ��c(di��n)��A��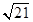 | B�� | C��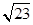 | D��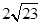 |
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ����Ԕ �}�ͣ�����}
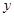 �S�ϵęE�AC1��
�S�ϵęE�AC1��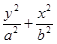 =1��(j��ng)�^(gu��)A(1��0)�c(di��n)�����x���ʞ�
=1��(j��ng)�^(gu��)A(1��0)�c(di��n)�����x���ʞ�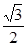 ��
��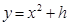 (h��R)��P�c(di��n)���о��c�E�AC1���ڃ��c(di��n)M��N��ӛ����MN�cPA�����c(di��n)�քe��G��H����(d��ng)GH�c
(h��R)��P�c(di��n)���о��c�E�AC1���ڃ��c(di��n)M��N��ӛ����MN�cPA�����c(di��n)�քe��G��H����(d��ng)GH�c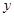 �Sƽ�Еr(sh��)����h����Сֵ��
�Sƽ�Еr(sh��)����h����Сֵ���鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ����Ԕ �}�ͣ�����}
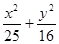 ��1���c(di��n)F1���ң���
��1���c(di��n)F1���ң��� ������
������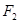 �ǙE�A���ҽ��c(di��n)���t��AB���L(zh��ng)��_______
�ǙE�A���ҽ��c(di��n)���t��AB���L(zh��ng)��_______�鿴�𰸺ͽ���>>
�ٶ����� - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o(w��)���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com