
2.A解析:由![]() 知函數在
知函數在![]() 上有零點,又因為函數在(0,+
上有零點,又因為函數在(0,+![]() )上是減函數,所以函數y=f(x) 在(0,+
)上是減函數,所以函數y=f(x) 在(0,+![]() )上有且只有一個零點不妨設為
)上有且只有一個零點不妨設為![]() ,則
,則![]() ,又因為函數是偶函數,所以
,又因為函數是偶函數,所以![]() =0并且函數在(0,+
=0并且函數在(0,+![]() )上是減函數,因此-
)上是減函數,因此-![]() 是(-
是(-![]() ,0)上的唯一零點,所以函數共有兩個零點
,0)上的唯一零點,所以函數共有兩個零點
下列敘述中,是隨機變量的有( )
①某工廠加工的零件,實際尺寸與規定尺寸之差;②標準狀態下,水沸騰的溫度;③某大橋一天經過的車輛數;④向平面上投擲一點,此點坐標.
A.②③ B.①② C.①③④ D.①③
科目:高中數學 來源: 題型:
| π |
| 6 |
| π |
| 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
(08年聊城市四模理) (12分) 已知M、N兩點的坐標分別是M(1+cos2x,1),N(1,![]() sin2x+a)(x,
sin2x+a)(x,![]() 是常數),令
是常數),令![]() 是坐標原點).
是坐標原點).
(1)求函數![]() 的解析式,并求函數
的解析式,并求函數![]() 在[0,π]上的單調遞增區間;
在[0,π]上的單調遞增區間;
(2)當![]() ,求a的值,并說明此時
,求a的值,并說明此時![]() 的圖象可由函數
的圖象可由函數
![]() 的圖象經過怎樣的平移和伸縮變換而得到.
的圖象經過怎樣的平移和伸縮變換而得到.
查看答案和解析>>
科目:高中數學 來源: 題型:
已知M、N兩點的坐標分別是![]() 是常數
是常數![]() ,令
,令![]() 是坐標原點
是坐標原點![]() .
.
(Ⅰ)求函數![]() 的解析式,并求函數
的解析式,并求函數![]() 在
在![]() 上的單調遞增區間;
上的單調遞增區間;
(Ⅱ)當![]() 時,
時,![]() 的最大值為
的最大值為![]() ,求a的值,并說明此時
,求a的值,并說明此時![]() 的圖象可由函數
的圖象可由函數![]() 的圖象經過怎樣的平移和伸縮變換而得到?
的圖象經過怎樣的平移和伸縮變換而得到?
查看答案和解析>>
科目:高中數學 來源:2013屆江西省高二下學期期中考試理科數學試卷(解析版) 題型:解答題
已知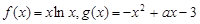
(1)求函數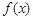 在
在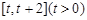 上的最小值
上的最小值
(2)對一切的 恒成立,求實數a的取值范圍
恒成立,求實數a的取值范圍
(3)證明對一切 ,都有
,都有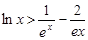 成立
成立
【解析】第一問中利用
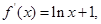 當
當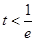 時,
時,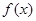 在
在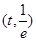 單調遞減,在
單調遞減,在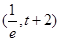 單調遞增
單調遞增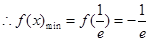 ,當
,當
 ,即
,即 時,
時,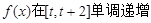 ,
,
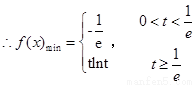
第二問中,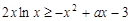 ,則
,則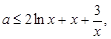 設
設 ,
,
則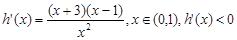 ,
, 單調遞增,
單調遞增, ,
, ,
, 單調遞減,
單調遞減,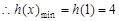 ,因為對一切
,因為對一切 ,
,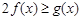 恒成立,
恒成立,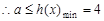
第三問中問題等價于證明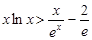 ,
, ,
,
由(1)可知 ,
, 的最小值為
的最小值為 ,當且僅當x=
,當且僅當x= 時取得
時取得
設 ,
, ,則
,則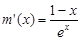 ,易得
,易得
 。當且僅當x=1時取得.從而對一切
。當且僅當x=1時取得.從而對一切 ,都有
,都有 成立
成立
解:(1)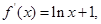 當
當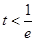 時,
時,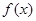 在
在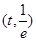 單調遞減,在
單調遞減,在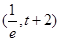 單調遞增
單調遞增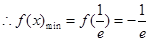 ,當
,當
 ,即
,即 時,
時,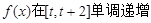 ,
,
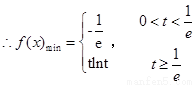 …………4分
…………4分
(2)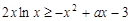 ,則
,則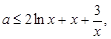 設
設 ,
,
則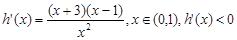 ,
, 單調遞增,
單調遞增, ,
, ,
, 單調遞減,
單調遞減,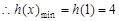 ,因為對一切
,因為對一切 ,
,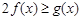 恒成立,
恒成立,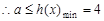 …………9分
…………9分
(3)問題等價于證明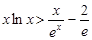 ,
, ,
,
由(1)可知 ,
, 的最小值為
的最小值為 ,當且僅當x=
,當且僅當x= 時取得
時取得
設 ,
, ,則
,則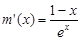 ,易得
,易得
 。當且僅當x=1時取得.從而對一切
。當且僅當x=1時取得.從而對一切 ,都有
,都有 成立
成立
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com