
已知函數f(x)=x3-ax2-3x.
(1)若f(x)在區間[1,+∞)上是增函數,求實數a的取值范圍;
(2)若x=-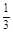 是f(x)的極值點,求f(x)在[1,a]上的最大值;
是f(x)的極值點,求f(x)在[1,a]上的最大值;
(3)在(2)的條件下,是否存在實數b,使得函數g(x)=bx的圖象與函數f(x)的圖象恰有3個交點,若存在,請求出實數b的取值范圍;若不存在,試說明理由.
(1)a≤0
(2)f(x)在[1,4]上的最大值是f(1)=-6
(3)存在,理由略
【解析】解 (1)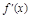 =3x2-2ax-3,∵f(x)在[1,+∞)上是增函數,
=3x2-2ax-3,∵f(x)在[1,+∞)上是增函數,
∴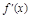 在[1,+∞)上恒有
在[1,+∞)上恒有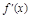 ≥0,
---------2分
≥0,
---------2分
即3x2-2ax-3≥0在[1,+∞)上恒成立.則必有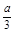 ≤1且
≤1且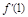 =-2a≥0, ,--------4分
=-2a≥0, ,--------4分
∴a≤0. ------------5分
(2)依題意,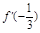 =0,即
=0,即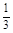 +
+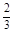 a-3=0,∴a=4,∴f(x)=x3-4x2-3x. ----------7分
a-3=0,∴a=4,∴f(x)=x3-4x2-3x. ----------7分
令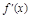 =3x2-8x-3=0,得x1=-
=3x2-8x-3=0,得x1=-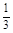 ,x2=3.則當x變化時,
,x2=3.則當x變化時,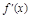 ,f(x)的變化情況如下表:
,f(x)的變化情況如下表:
|
x |
1 |
(1,3) |
3 |
(3,4) |
4 |
|
|
|
- |
0 |
+ |
|
|
f(x) |
-6 |
↘ |
-18 |
↗ |
-12 |
----9分
∴f(x)在[1,4]上的最大值是f(1)=-6. -----------10分
(3)函數g(x)=bx的圖象與函數f(x)的圖象恰有3個交點,即方程x3-4x2-3x=bx恰有3個不等實根∴x3-4x2-3x-bx=0,∴x=0是其中一個根 -------------12分
∴方程x2-4x-3-b=0有兩個非零不等實根,∴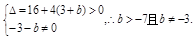
∴存在符合條件的實數b,b的范圍為b>-7且b≠-3. -----------14分


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源: 題型:
| x |
| a |
| b |
| x |
| 4c2 |
| k(k+c) |
查看答案和解析>>
科目:高中數學 來源:浙江省東陽中學高三10月階段性考試數學理科試題 題型:022
已知函數f(x)的圖像在[a,b]上連續不斷,f1(x)=min{f(t)|a≤t≤x}(x∈[a,b]),f2(x)=max{f(t)|a≤t≤x}(x∈[a,b]),其中,min{f(x)|x∈D}表示函數f(x)在D上的最小值,max{f(x)|x∈D}表示函數f(x)在D上的最大值,若存在最小正整數k,使得f2(x)-f1(x)≤k(x-a)對任意的x∈[a,b]成立,則稱函數f(x)為[a,b]上的“k階收縮函數”.已知函數f(x)=x2,x∈[-1,4]為[-1,4]上的“k階收縮函數”,則k的值是_________.
查看答案和解析>>
科目:高中數學 來源:上海模擬 題型:解答題
| x |
| a |
| b |
| x |
| 4c2 |
| k(k+c) |
查看答案和解析>>
科目:高中數學 來源:2009-2010學年河南省許昌市長葛三高高三第七次考試數學試卷(理科)(解析版) 題型:選擇題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com