已知向量a＝(3，－2)，b＝(－2，1)，c＝(5，－3)，試用a和b來表示c．
答案：
解析：
|
解：設c＝ma＋nb，
即(5，－3)＝m(3，－2)＋n(－2，1)＝(3m－2n，－2m＋n)，
于是有 解得
所以c＝a－b．
思路分析：設c＝ma＋nb，然后利用待定系數法求出m、n的值．
|
練習冊系列答案
相關習題
科目：高中數學
來源：設計必修四數學北師版 北師版
題型：013
已知向量a＝(3，4)，b＝(sinα，cosα)，且a∥b，則tanα的值為
[ ]
A．
B．
C．
D．
查看答案和解析>>
科目：高中數學
來源：設計必修四數學人教A版 人教A版
題型：013
已知向量a＝(3，2)，b＝(x，4)，且a∥b，則x的值為
[ ]
C．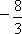
D．
查看答案和解析>>
科目：高中數學
來源：重難點手冊 高中數學·必修4（配人教A版新課標） 人教A版新課標
題型：044
已知向量a＝(3，4)，b＝(2，－1)，向量(a＋mb)⊥(a－b)，求m的值．
查看答案和解析>>
科目：高中數學
來源：導學大課堂選修數學2-1蘇教版 蘇教版
題型：044
已知向量a＝(3，－2，1)，b＝(－2，4，0)，c＝(3，0，2)，求a－2b＋4c．
查看答案和解析>>
科目：高中數學
來源：導學大課堂必修四數學蘇教版 蘇教版
題型：044
已知向量a＝(3，－2)，b＝(－2，1)，c＝(7，－4)．試用a和b來表示c．
查看答案和解析>>
開心快樂假期作業暑假作業西安出版社系列答案
名題訓練系列答案
期末集結號系列答案
