
【題目】甘肅省是土地荒漠化較為嚴重的省份,一代代治沙人為了固沙、治沙,改善生態環境,不斷地進行研究與實踐,實現了沙退人進.![]() 年,古浪縣八步沙林場“六老漢”三代人治沙群體作為優秀代表,被中宣部授予“時代楷模”稱號.在治沙過程中為檢測某種固沙方法的效果,治沙人在某一實驗沙丘的坡頂和坡腰各布設了
年,古浪縣八步沙林場“六老漢”三代人治沙群體作為優秀代表,被中宣部授予“時代楷模”稱號.在治沙過程中為檢測某種固沙方法的效果,治沙人在某一實驗沙丘的坡頂和坡腰各布設了![]() 個風蝕插釬,以測量風蝕值.(風蝕值是測量固沙效果的指標之一,數值越小表示該插釬處被風吹走的沙層厚度越小,說明固沙效果越好,數值為
個風蝕插釬,以測量風蝕值.(風蝕值是測量固沙效果的指標之一,數值越小表示該插釬處被風吹走的沙層厚度越小,說明固沙效果越好,數值為![]() 表示該插釬處沒有被風蝕)通過一段時間的觀測,治沙人記錄了坡頂和坡腰全部插釬測得的風蝕值(所測數據均不為整數),并繪制了相應的頻率分布直方圖.
表示該插釬處沒有被風蝕)通過一段時間的觀測,治沙人記錄了坡頂和坡腰全部插釬測得的風蝕值(所測數據均不為整數),并繪制了相應的頻率分布直方圖.
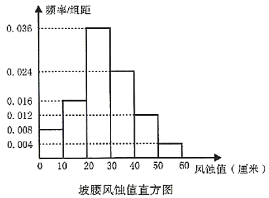
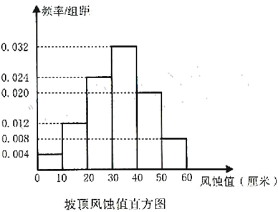
(Ⅰ)根據直方圖估計“坡腰處一個插釬風蝕值小于![]() ”的概率;
”的概率;
(Ⅱ)若一個插釬的風蝕值小于![]() ,則該數據要標記“
,則該數據要標記“![]() ”,否則不標記根據以上直方圖,完成列聯表:
”,否則不標記根據以上直方圖,完成列聯表:
標記 | 不標記 | 合計 | |
坡腰 | |||
坡頂 | |||
合計 |
并判斷是否有![]() 的把握認為數據標記“
的把握認為數據標記“![]() ”與沙丘上插釬所布設的位置有關?
”與沙丘上插釬所布設的位置有關?
附: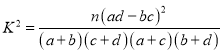 .
.
|
|
|
|
|
|
|
|
科目:高中數學 來源: 題型:
【題目】四棱錐S-ABCD中,底面ABCD是邊長為2的菱形,![]() ,
,![]() ,二面角S-BD-C的余弦值為
,二面角S-BD-C的余弦值為![]() .
.
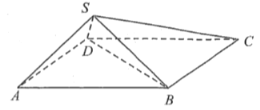
(I)證明:平面![]() 平面SBD;
平面SBD;
(Ⅱ)求二面角A-SD-C的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓錐的頂點為A,高和底面的半徑相等,BE是底面圓的一條直徑,點D為底面圓周上的一點,且∠ABD=60°,則異面直線AB與DE所成角的正弦值為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,直線l的參數方程為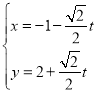 (t為參數),以坐標原點O為極點,x軸的正半軸為極軸建立極坐標系,曲線C1的極坐標方程為
(t為參數),以坐標原點O為極點,x軸的正半軸為極軸建立極坐標系,曲線C1的極坐標方程為![]() ,曲線C2的直角坐標方程為
,曲線C2的直角坐標方程為![]() .
.
(1)若直線l與曲線C1交于M、N兩點,求線段MN的長度;
(2)若直線l與x軸,y軸分別交于A、B兩點,點P在曲線C2上,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某城市在進行創建文明城市的活動中,為了解居民對“創建文明城”的滿意程度,組織居民給活動打分(分數為整數,滿分100分),從中隨機抽取一個容量為120的樣本,發現所給數據均在[40,100]內.現將這些分數分成以下6組并畫出樣本的頻率分布直方圖,但不小心污損了部分圖形,如圖所示.觀察圖形則下列說法中有錯誤的是( )
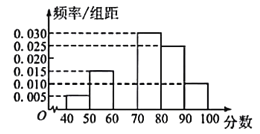
A.第三組的頻數為18人
B.根據頻率分布直方圖估計眾數為75分
C.根據頻率分布直方圖估計樣本的平均數為75分
D.根據頻率分布直方圖估計樣本的中位數為75分
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐S﹣ABCD中,側面SCD為鈍角三角形且垂直于底面ABCD,CD=SD,點M是SA的中點,AD//BC,∠ABC=90°,AB=AD![]() BC=a.
BC=a.

(1)求證:平面MBD⊥平面SCD;
(2)若∠SDC=120°,求三棱錐C﹣MBD的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知直線![]() :
:![]() ,半徑為2的圓
,半徑為2的圓![]() 與
與![]() 相切,圓心
相切,圓心![]() 在
在![]() 軸上且在直線
軸上且在直線![]() 的右上方.
的右上方.
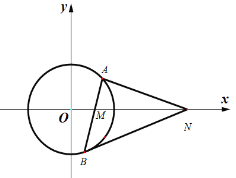
(1)求圓![]() 的方程;
的方程;
(2)過點![]() 的直線與圓
的直線與圓![]() 交于
交于![]() ,
,![]() 兩點(
兩點(![]() 在
在![]() 軸上方),問在
軸上方),問在![]() 軸正半軸上是否存在定點
軸正半軸上是否存在定點![]() ,使得
,使得![]() 軸平分
軸平分![]() ?若存在,請求出點
?若存在,請求出點![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,已知四邊形
中,已知四邊形![]() 是邊長為
是邊長為![]() 的正方形,點
的正方形,點![]() 在底面
在底面![]() 上的射影為底面
上的射影為底面![]() 的中心點
的中心點![]() ,點
,點![]() 在棱
在棱![]() 上,且
上,且![]() 的面積為1.
的面積為1.
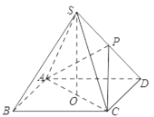
(1)若點![]() 是
是![]() 的中點,求證:平面
的中點,求證:平面![]() 平面
平面![]() ;
;
(2)在棱![]() 上是否存在一點
上是否存在一點![]() 使得二面角
使得二面角![]() 的余弦值為
的余弦值為![]() ?若存在,求出點
?若存在,求出點![]() 的位置;若不存在,說明理由.
的位置;若不存在,說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com