
【題目】某學校舉行知識競賽,第一輪選拔共設有A、B、C、D四個問題,規則如下:
①每位參加者記分器的初始分均為10分,答對問題A、B、C、D分別加1分、2分、3分、6分,答錯任一題減2分;
②每回答一題,記分器顯示累計分數,當累計分數小于8分時,答題結束,淘汰出局;當累計分數大于或等于14分時,答題結束,進入下一輪;當答完四題,累計分數仍不足14分時,答題結束,淘汰出局;
③每位參加者按問題A、B、C、D順序作答,直至答題結束.
假設甲同學對問題A、B、C、D回答正確的概率依次為![]() 、
、![]() 、
、![]() 、
、![]() ,且各題回答正確與否相互之間沒有影響.
,且各題回答正確與否相互之間沒有影響.
(1)求甲同學能進入下一輪的概率;
(2)用ξ表示甲同學本輪答題結束時答題的個數,求ξ的分布列和數學期望Εξ.
【答案】(1)![]() ;(2) 分布列見解析,期望為
;(2) 分布列見解析,期望為![]()
【解析】
(1)根據題意,列舉甲能進入下一輪的五種情況,由于每題答題結果相互獨立,根據相互對立事件和互斥事件的概率公式,得到結果;
(2)喲圖一可知答對一個題或答錯一個題都不能決定你甲的去留,所以最少答兩個題,隨機變量![]() 可能的取值為
可能的取值為![]() ,由于每題的答題結構都是相對獨立的,根據相互對立事件同時發生的概率得到結果.
,由于每題的答題結構都是相對獨立的,根據相互對立事件同時發生的概率得到結果.
設![]() 分別是第一、二、三、四個問題,用
分別是第一、二、三、四個問題,用![]() 表示甲同學第
表示甲同學第![]() 個問題回答正確,用
個問題回答正確,用![]() 表示第
表示第![]() 個問題回答錯誤,則
個問題回答錯誤,則![]() 是對立事件,
是對立事件,
由題意得,![]() ,
,
則![]() ,
,
(1)記“甲同學能進入下一輪”為事件Q,
則![]()
![]()
![]() .
.
(2)由題意,可知隨機變量![]() 可能的取值
可能的取值![]() ,
,
由于每題答題結果都是相對對立的,
因為![]() ,
,
![]()
![]() ,
,
| 2 | 3 | 4 |
|
|
|
|
所以![]() .
.


科目:高中數學 來源: 題型:
【題目】定義在![]() 上的函數
上的函數![]() ,
,![]() 單調遞增,
單調遞增,![]() ,若對任意
,若對任意![]() ,存在
,存在![]() ,使得
,使得![]() 成立,則稱
成立,則稱![]() 是
是![]() 在
在![]() 上的“追逐函數”.若
上的“追逐函數”.若![]() ,則下列四個命題:①
,則下列四個命題:①![]() 是
是![]() 在
在![]() 上的“追逐函數”;②若
上的“追逐函數”;②若![]() 是
是![]() 在
在![]() 上的“追逐函數”,則
上的“追逐函數”,則![]() ;③
;③![]() 是
是![]() 在
在![]() 上的“追逐函數”;④當
上的“追逐函數”;④當![]() 時,存在
時,存在![]() ,使得
,使得![]() 是
是![]() 在
在![]() 上的“追逐函數”.其中正確命題的個數為( )
上的“追逐函數”.其中正確命題的個數為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設![]() 是拋物線
是拋物線![]() 上的一點,拋物線
上的一點,拋物線![]() 在點
在點![]() 處的切線方程為
處的切線方程為![]() .
.
(1)求![]() 的方程;
的方程;
(2)已知過點![]() 的兩條不重合直線
的兩條不重合直線![]() ,
,![]() 的斜率之積為
的斜率之積為![]() ,且直線
,且直線![]() ,
,![]() 分別交拋物線
分別交拋物線![]() 于
于![]() ,
,![]() 兩點和
兩點和![]() ,
,![]() 兩點.是否存在常數
兩點.是否存在常數![]() 使得
使得![]() 成立?若存在,求出
成立?若存在,求出![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在多面體ABCDEF中,四邊形ADEF為正方形,AD∥BC,AD⊥AB,AD=2BC=2.
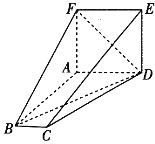
(1)證明:平面ADEF⊥平面ABF.
(2)若平面ADEF⊥平面ABCD,二面角A-BC-E為30°,三棱錐A-BDF的外接球的球心為O,求異面直線OC與DF所成角的余弦值
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】從一批蘋果中,隨機抽取50個,其重量(單位:克)的頻數分布表如下:
分組(重量) |
|
|
|
|
頻數(個) | 5 | 10 | 20 | 15 |
(1) 根據頻數分布表計算蘋果的重量在![]() 的頻率;
的頻率;
(2) 用分層抽樣的方法從重量在![]() 和
和![]() 的蘋果中共抽取4個,其中重量在
的蘋果中共抽取4個,其中重量在![]() 的有幾個?
的有幾個?
(3) 在(2)中抽出的4個蘋果中,任取2個,求重量在![]() 和
和![]() 中各有1個的概率.
中各有1個的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某市為了了解民眾對開展創建文明城市工作以來的滿意度,隨機調查了40名群眾,并將他們隨機分成![]() ,
,![]() 兩組,每組20人,
兩組,每組20人,![]() 組群眾給第一階段的創文工作評分,
組群眾給第一階段的創文工作評分,![]() 組群眾給第二階段的創文工作評分,根據兩組群眾的評分繪制了如圖所示的莖葉圖.
組群眾給第二階段的創文工作評分,根據兩組群眾的評分繪制了如圖所示的莖葉圖.
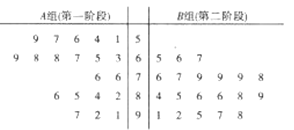
(Ⅰ)根據莖葉圖比較群眾對兩個階段的創文工作滿意度評分的平均值和集中程度(不要求計算出具體值,給出結論即可);
(Ⅱ)完成下面的列聯表,并通過計算判斷是否有![]() 的把握認為民眾對兩個階段創文工作的滿意度存在差異?
的把握認為民眾對兩個階段創文工作的滿意度存在差異?
低于70分 | 不低于70分 | 合計 | |
第一階段 | |||
第二階段 | |||
合計 |
參考公式:![]() ,
,![]() .
.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,矩形![]() 中,
中,![]() ,
,![]() 為邊
為邊![]() 的中點,沿
的中點,沿![]() 將
將![]() 折起,點
折起,點![]() 折至
折至![]() 處(
處(![]() 平面
平面![]() ),若
),若![]() 為線段
為線段![]() 的中點,則在
的中點,則在![]() 折起過程中,下列說法錯誤的是( )
折起過程中,下列說法錯誤的是( )
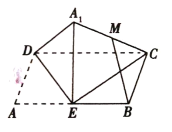
A.始終有![]() 平面
平面![]()
B.不存在某個位置,使得![]() 面
面![]()
C.點![]() 在某個球面上運動
在某個球面上運動
D.一定存在某個位置,使得異面直線![]() 與
與![]() 所成角為
所成角為![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】△ABC的內角A,B,C的對邊分別為a,b,c,且(![]() b+c)tanC=﹣ctanA.
b+c)tanC=﹣ctanA.
(1)求A;
(2)若b![]() ,c=2,點D在BC邊上,且AD=BD,求AD的長.
,c=2,點D在BC邊上,且AD=BD,求AD的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com