
在數列 中,
中,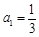 ,且前
,且前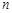 項的算術平均數等于第
項的算術平均數等于第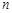 項的
項的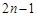 倍(
倍( )。
)。
(1)寫出此數列的前5項; (2)歸納猜想 的通項公式,并加以證明。
的通項公式,并加以證明。
(1)數列的前5項是: ,
, .(2)見解析.
.(2)見解析.
【解析】(1)本小題根據題意可得 ,分別令n=2,3,4,5不難求解。
,分別令n=2,3,4,5不難求解。
(2)由(1)中的前5項,不難歸納出 ,然后再采用數學歸納法進行證明。
,然后再采用數學歸納法進行證明。
要分兩個步驟來進行:第一步驗證:當n=1時,式子成立;
第二步:先假設n=k時,等式成立,再證明n=k+1時,等式也成立,在證明過程中必須要用上歸納假設。
(1)由已知 ,
, ,分別取
,分別取 ,
,
得 ,
, ,
,
 ,
,
 ,
,
所以數列的前5項是: ,
, .-----------4分
.-----------4分
(2)由(1)中的分析可以猜想 .————————————6分
.————————————6分
下面用數學歸納法證明:
①當 時,公式顯然成立.
時,公式顯然成立.
②假設當 時成立,即
時成立,即 ,那么由已知,
,那么由已知,
得 ,
,
即 ,
,
所以 ,即
,即 ,
,
又由歸納假設,得 ,
,
所以 ,即當
,即當 時,公式也成立.—————————10分
時,公式也成立.—————————10分
由①和②知,對一切 ,都有
,都有 成立.------------------12分
成立.------------------12分


 捷徑訓練檢測卷系列答案
捷徑訓練檢測卷系列答案 小夫子全能檢測系列答案
小夫子全能檢測系列答案科目:高中數學 來源:2013屆福建省高二下學期期中考試理科數學試卷(解析版) 題型:解答題
(本小題滿分14分)
在數列 中,
中,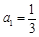 ,且前
,且前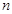 項的算術平均數等于第
項的算術平均數等于第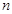 項的
項的 倍(
倍( ). (即
). (即
(1)寫出此數列的前5項;
(2)歸納猜想 的通項公式,并加以證明.
的通項公式,并加以證明.
查看答案和解析>>
科目:高中數學 來源:2012屆山東省高二下學期期末考試理科數學 題型:解答題
(本題滿分13分)
在數列 中,
中, ,且前
,且前 項的算術平均數等于第
項的算術平均數等于第 項的
項的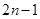 倍
倍 .
.
(1)寫出此數列的前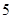 項;
項;
(2)歸納猜想 的通項公式,并用數學歸納法證明.
的通項公式,并用數學歸納法證明.
查看答案和解析>>
科目:高中數學 來源:2012屆安徽省亳州市高二第二學期期末質量檢測理科數學試題 題型:解答題
在數列 中,
中, ,且前
,且前 項的算術平均數等于第
項的算術平均數等于第 項的
項的 倍
倍 .
.
(1)寫出此數列的前 項;
項;
(2)歸納猜想 的通項公式,并用數學歸納法證明
的通項公式,并用數學歸納法證明
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com