已知函數f(x)=x2+ax+2ln(x-1),a是常數.
(1)證明曲線y=f(x)在點(2,f(2))的切線經過y軸上一個定點;
(2)若f′(x)>(a-3)x2對?x∈(2,3)恒成立,求a的取值范圍;
(參考公式:3x3-x2-2x+2=(x+1)(3x2-4x+2))
(3)討論函數f(x)的單調區間.
解:(1)f(2)=2a+4,
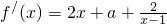
,…(1分) f′(2)=6+a…(2分),
曲線y=f(x)在點(2,f(2))的切線為y-(2a+4)=(6+a)(x-2)…(3分),
當x=0時,由切線方程得y=-8,所以切線經過y軸上的定點(0,-8)…(4分).
(2)由f′(x)>(a-3)x
2得

…(5分),
對?x∈(2,3),x
2-1>0,
所以
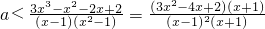
=
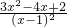
…(6分),
設
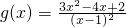
,則

…(7分)
g(x)在區間(2,3)單調遞減…(8分),
所以
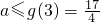
,a的取值范圍為
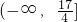
…(9分).
(3)函數f(x)=x
2+ax+2ln(x-1)的定義域為(1,+∞),
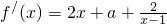
=
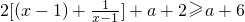
…(10分).
若a≥-6,則f′(x)≥0,f(x)在定義域(1,+∞)上單調增加…(11分);
若a<-6,解方程
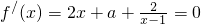
得
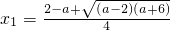
,
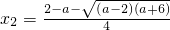
…(12分),
x
1>x
2>1,當x>x
1或1<x<x
2時,f′(x)>0;
當x
2<x<x
1時,f′(x)<0…(13分),
所以f(x)的單調增區間是(1,x
2)和(x
1,+∞),
單調減區間是[x
2,x
1](區間無論包含端點x
1、x
2均可,但要前后一致)…(14分)
分析:(1)先根據題意求出切點與函數的導數,再結合導數的幾何意義求出切線的斜率,進而求出切線的方程.
(2)先把問題轉化為
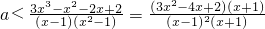
恒成立,然后求出不等式右邊的最小值即可求出實數a的取值范圍;
(3)在函數 的定義域內解不等式fˊ(x)>0和fˊ(x)<0,確定 的單調區間.若在函數式中含字母系數,往往要分類討論.
點評:本題主要考查函數恒成立問題以及轉化思想的應用和計算能力,屬于對知識和思想方法的綜合考查,屬于中檔題.對于第三問要注意到參數的取值范圍對導數的符號有影響故需要對參數分類討論,而第二問中關鍵是把函數是減函數的性質轉化為函數恒成立的問題,轉化思想在高中數學在應用很廣泛.

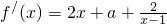 ,…(1分) f′(2)=6+a…(2分),
,…(1分) f′(2)=6+a…(2分), …(5分),
…(5分),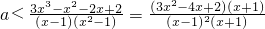
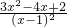 …(6分),
…(6分),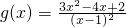 ,則
,則 …(7分)
…(7分)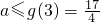 ,a的取值范圍為
,a的取值范圍為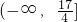 …(9分).
…(9分).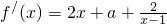
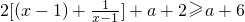 …(10分).
…(10分).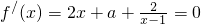 得
得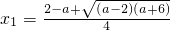 ,
,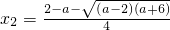 …(12分),
…(12分),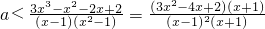 恒成立,然后求出不等式右邊的最小值即可求出實數a的取值范圍;
恒成立,然后求出不等式右邊的最小值即可求出實數a的取值范圍;

 已知函數f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函數f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<