
【題目】如下圖所示的幾何體中, ![]() 為三棱柱,且
為三棱柱,且![]() ,四邊形
,四邊形![]() 為平行四邊形,
為平行四邊形, ![]() ,
, ![]() .
.
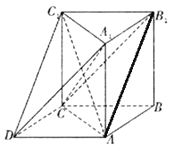
(1)求證: ![]() ;
;
(2)若![]() ,求證:
,求證: ![]() ;
;
(3)若![]() ,二面角
,二面角![]() 的余弦值為若
的余弦值為若![]() ,求三棱錐
,求三棱錐![]() 的體積.
的體積.
科目:高中數學 來源: 題型:
【題目】已知a>0,a≠1且loga3>loga2,若函數f(x)=logax在區間[a,2a]上的最大值與最小值之差為1.
(1)求a的值;
(2)解不等式 ![]() ;
;
(3)求函數g(x)=|logax﹣1|的單調區間.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某種零件按質量標準分為1,2,3,4,5五個等級,現從一批該零件巾隨機抽取20個,對其等級進行統計分析,得到頻率分布表如下
等級 | 1 | 2 | 3 | 4 | 5 |
頻率 | 0.05 | m | 0.15 | 0.35 | n |
(1)在抽取的20個零件中,等級為5的恰有2個,求m,n;
(2)在(1)的條件下,從等級為3和5的所有零件中,任意抽取2個,求抽取的2個零件等級恰好相同的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在直三棱柱ABC﹣A1B1C1中,AB=BC=2AA1 , ∠ABC=90°,D是BC的中點.
(1)求證:A1B∥平面ADC1;
(2)求二面角C1﹣AD﹣C的余弦值;
(3)試問線段A1B1上是否存在點E,使AE與DC1成60°角?若存在,確定E點位置,若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數f(x)=x2ex﹣1﹣ ![]() x3﹣x2(x∈R).
x3﹣x2(x∈R).
(1)求函數f(x)的單調區間;
(2)當x∈(1,+∞)時,用數學歸納法證明:n∈N* , ex﹣1> ![]() (其中n!=1×2×…×n).
(其中n!=1×2×…×n).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知在等比數列{an}中,a1=1,且a2是a1和a3﹣1的等差中項.
(1)求數列{an}的通項公式;
(2)若數列{bn}滿足bn=2n﹣1+an(n∈N*),求{bn}的前n項和Sn .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知直線l經過點P(2,﹣1),且在兩坐標軸上的截距之和為2,圓M的圓心在直線2x+y=0上,且與直線l相切于點P.
(1)求直線l的方程;
(2)求圓M的方程;
(3)求圓M在y軸上截得的弦長.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某同學在上學路上要經過![]() 、
、![]() 、
、![]() 三個帶有紅綠燈的路口.已知他在
三個帶有紅綠燈的路口.已知他在![]() 、
、![]() 、
、![]() 三個路口遇到紅燈的概率依次是
三個路口遇到紅燈的概率依次是![]() 、
、![]() 、
、![]() ,遇到紅燈時停留的時間依次是
,遇到紅燈時停留的時間依次是![]() 秒、
秒、![]() 秒、
秒、![]() 秒,且在各路口是否遇到紅燈是相互獨立的.
秒,且在各路口是否遇到紅燈是相互獨立的.
(1)求這名同學在上學路上在第三個路口首次遇到紅燈的概率;,
(2)求這名同學在上學路上因遇到紅燈停留的總時間.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數y=f(x)的定義域為{x|x∈R,且x≠2},且y=f(x+2)是偶函數,當x<2時,f(x)=|2x﹣1|,那么當x>2時,函數f(x)的遞減區間是( )
A.(3,5)
B.(3,+∞)
C.(2,+∞)
D.(2,4]
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com