
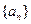 的前
的前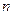 項(xiàng)和為
項(xiàng)和為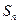 ,對(duì)一切
,對(duì)一切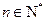 ,點(diǎn)
,點(diǎn)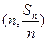 都在函數(shù)
都在函數(shù)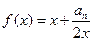 的圖象上. (1) 求數(shù)列
的圖象上. (1) 求數(shù)列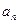 的通項(xiàng)公式; (2) 將數(shù)列
的通項(xiàng)公式; (2) 將數(shù)列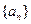 依次按1項(xiàng)、2項(xiàng)、3項(xiàng)、4項(xiàng)循環(huán)地分為(
依次按1項(xiàng)、2項(xiàng)、3項(xiàng)、4項(xiàng)循環(huán)地分為(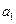 ),(
),(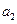 ,
,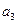 ),(
),(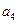 ,
,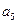 ,
,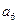 ),(
),(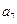 ,
,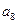 ,
,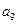 ,
,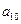 );(
);(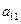 ),(
),(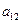 ,
,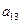 ),(
),(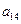 ,
,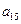 ,
,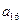 ),(
),(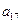 ,
,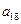 ,
,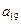 ,
,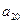 );(
);(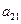 ),…,分別計(jì)算各個(gè)括號(hào)內(nèi)各數(shù)之和,設(shè)由這些和按原來(lái)括號(hào)的前后順序構(gòu)成的數(shù)列為
),…,分別計(jì)算各個(gè)括號(hào)內(nèi)各數(shù)之和,設(shè)由這些和按原來(lái)括號(hào)的前后順序構(gòu)成的數(shù)列為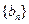 ,求
,求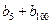 的值;(3)設(shè)
的值;(3)設(shè)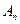 為數(shù)列
為數(shù)列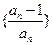 的前
的前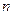 項(xiàng)積,若不等式
項(xiàng)積,若不等式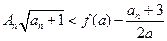 對(duì)一切
對(duì)一切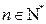 都成立,求
都成立,求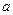 的取值范圍.
的取值范圍.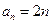 (Ⅱ)
(Ⅱ) 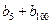 ="2010 " (Ⅲ)
="2010 " (Ⅲ)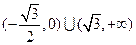
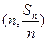 在函數(shù)
在函數(shù)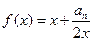 的圖象上,故
的圖象上,故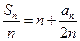 ,
,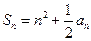 .令
.令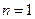 ,得
,得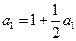 ,所以
,所以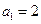 ;令
;令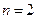 ,得
,得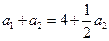 ,所以
,所以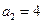 ;令
;令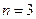 ,得
,得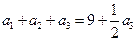 ,所以
,所以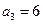 .由此猜想:
.由此猜想: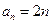 .
. 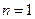 時(shí),有上面的求解知,猜想成立.
時(shí),有上面的求解知,猜想成立. 時(shí)猜想成立,即
時(shí)猜想成立,即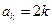 成立,
成立,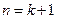 時(shí),注意到
時(shí),注意到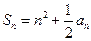
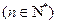 ,
,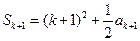 ,
,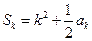 .
.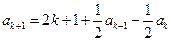 ,所以
,所以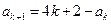 .
.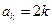 ,故
,故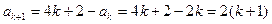 .
.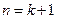 時(shí),猜想也成立.由①②知,對(duì)一切
時(shí),猜想也成立.由①②知,對(duì)一切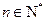 ,
,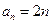 成立 .
成立 . 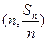 在函數(shù)
在函數(shù)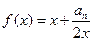 的圖象上,
的圖象上,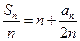 ,所以
,所以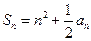 ①.令
①.令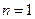 ,得
,得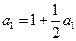 ,所以
,所以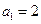 ;
; 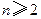 時(shí)
時(shí)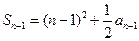 ②
②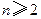 時(shí)①-②得
時(shí)①-②得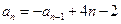
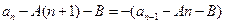 ,即
,即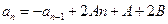 與
與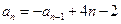 比較可得
比較可得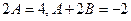 ,解得
,解得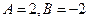 .因此
.因此
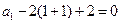 ,所以
,所以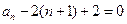 ,從而
,從而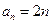 .
. 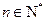 ),所以數(shù)列
),所以數(shù)列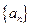 依次按1項(xiàng)、2項(xiàng)、3項(xiàng)、4項(xiàng)循環(huán)地分為(2),(4,6),(8,10,12),(14,16,18,20);(22),(24,26),(28,30,32),(34,36,38,40);(42),…. 每一次循環(huán)記為一組.由于每一個(gè)循環(huán)含有4個(gè)括號(hào), 故
依次按1項(xiàng)、2項(xiàng)、3項(xiàng)、4項(xiàng)循環(huán)地分為(2),(4,6),(8,10,12),(14,16,18,20);(22),(24,26),(28,30,32),(34,36,38,40);(42),…. 每一次循環(huán)記為一組.由于每一個(gè)循環(huán)含有4個(gè)括號(hào), 故 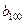 是第25組中第4個(gè)括號(hào)內(nèi)各數(shù)之和.由分組規(guī)律知,由各組第4個(gè)括號(hào)中所有第1個(gè)數(shù)組成的數(shù)列是等差數(shù)列,且公差為20. 同理,由各組第4個(gè)括號(hào)中所有第2個(gè)數(shù)、所有第3個(gè)數(shù)、所有第4個(gè)數(shù)分別組成的數(shù)列也都是等差數(shù)列,且公差均為20. 故各組第4個(gè)括號(hào)中各數(shù)之和構(gòu)成等差數(shù)列,且公差為80. 注意到第一組中第4個(gè)括號(hào)內(nèi)各數(shù)之和是68,所以
是第25組中第4個(gè)括號(hào)內(nèi)各數(shù)之和.由分組規(guī)律知,由各組第4個(gè)括號(hào)中所有第1個(gè)數(shù)組成的數(shù)列是等差數(shù)列,且公差為20. 同理,由各組第4個(gè)括號(hào)中所有第2個(gè)數(shù)、所有第3個(gè)數(shù)、所有第4個(gè)數(shù)分別組成的數(shù)列也都是等差數(shù)列,且公差均為20. 故各組第4個(gè)括號(hào)中各數(shù)之和構(gòu)成等差數(shù)列,且公差為80. 注意到第一組中第4個(gè)括號(hào)內(nèi)各數(shù)之和是68,所以 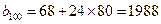 .又
.又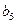 =22,所以
=22,所以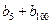 =2010.
=2010.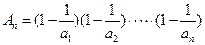 ,
,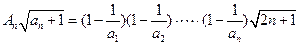 .
.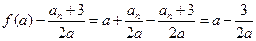 ,
,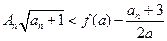 對(duì)一切
對(duì)一切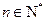 都成立,就是
都成立,就是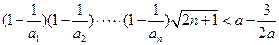 對(duì)一切
對(duì)一切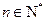 都成立.……………9分
都成立.……………9分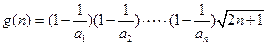 ,則只需
,則只需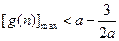 即可.
即可.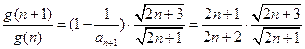
 ,
,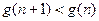 ,故
,故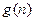 是單調(diào)遞減,于是
是單調(diào)遞減,于是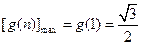 .
.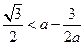 即
即 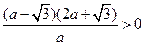 ,解得
,解得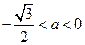 ,或
,或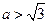 .
.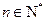 都成立的實(shí)數(shù)
都成立的實(shí)數(shù)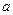 的取值范圍是
的取值范圍是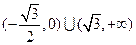


 科學(xué)實(shí)驗(yàn)活動(dòng)冊(cè)系列答案
科學(xué)實(shí)驗(yàn)活動(dòng)冊(cè)系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源:不詳 題型:解答題
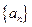 的前n項(xiàng)積為
的前n項(xiàng)積為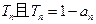 ;數(shù)列
;數(shù)列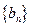 的前n項(xiàng)和為
的前n項(xiàng)和為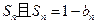 .
.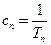 .①證明數(shù)列
.①證明數(shù)列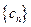 成等差數(shù)列;②求證數(shù)列
成等差數(shù)列;②求證數(shù)列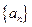 的通項(xiàng)公式;
的通項(xiàng)公式;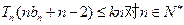 恒成立,求實(shí)數(shù)k的取值范圍.
恒成立,求實(shí)數(shù)k的取值范圍.查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源:不詳 題型:解答題
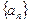 中,已知
中,已知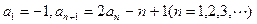
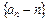 是等比數(shù)列
是等比數(shù)列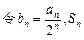 為數(shù)列
為數(shù)列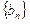 的前
的前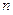 項(xiàng)和,求
項(xiàng)和,求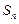 的表達(dá)式
的表達(dá)式查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源:不詳 題型:單選題
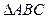 的三內(nèi)角A、B、C成等差數(shù)列,sinA 、sinB、 sinC成等比數(shù)列,則這個(gè)三角形的形狀是( )
的三內(nèi)角A、B、C成等差數(shù)列,sinA 、sinB、 sinC成等比數(shù)列,則這個(gè)三角形的形狀是( )查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源:不詳 題型:單選題
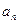 }中的首項(xiàng)
}中的首項(xiàng)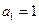 ,且滿足
,且滿足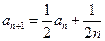 ,則此數(shù)列的第3項(xiàng)是( )
,則此數(shù)列的第3項(xiàng)是( )| A.1 | B.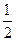 | C.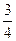 | D.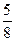 |
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com