
 x2+mx+
x2+mx+ (m<0),直線l與函數f(x)、g(x)的圖象都相切,且與函數f(x)的圖象的切點的橫坐標為1.
(m<0),直線l與函數f(x)、g(x)的圖象都相切,且與函數f(x)的圖象的切點的橫坐標為1. ),然后記a-b=t,(t>0),得a=b+t,將所得的差化為以b和t為單位的式子,再記
),然后記a-b=t,(t>0),得a=b+t,將所得的差化為以b和t為單位的式子,再記 ,F(s)=ln(1+s)-s,通過討論其單調性得ln(1+s)<s,最后將此不等式還原為以b和t為單位的式子,運用不等式的性質進行放縮,可得a-b+2aln(
,F(s)=ln(1+s)-s,通過討論其單調性得ln(1+s)<s,最后將此不等式還原為以b和t為單位的式子,運用不等式的性質進行放縮,可得a-b+2aln( )<0,最終得到a+2af(a+b)<b+2af(2a).
)<0,最終得到a+2af(a+b)<b+2af(2a). ,所以切線斜率為k=f′(1)=1
,所以切線斜率為k=f′(1)=1 ⇒m=-2或4
⇒m=-2或4 (x>-1)
(x>-1) )
) )=t+2(b+t)ln[
)=t+2(b+t)ln[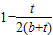 ]
] ,(-1<s<0),
,(-1<s<0), >0
>0 ]<t+2(b+t)
]<t+2(b+t)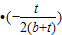 =t-t=0
=t-t=0 )<0
)<0

 激活思維優加課堂系列答案
激活思維優加課堂系列答案 活力試卷系列答案
活力試卷系列答案科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源: 題型:
| 2(x-1) |
| x+1 |
| x1+x2 |
| 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| 1 |
| f(n) |
查看答案和解析>>
科目:高中數學 來源: 題型:
| ||
| a |
| ||
| x |
| 6 |
| 6 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com