【答案】
分析:本題考查了互為反函數的函數圖象之間的關系、求反函數的方法、解方程組等知識和方法;根據點(1,2)在
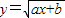
的圖象上,又在它的反函數的圖象上,可以有兩種方法求解:
法一:求出反函數,將點(1,2)分別代入原函數和反函數的方程,構建方程組解得;
法二:利用互為反函數的函數圖象關于y=x對稱這一特點,不求反函數,直接將點(1,2)和關于y=x的對稱點(2,1)分別代入原函數解析式構建方程組獲得.
解答:解:法一:由已知得:
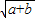
=2,即a+b=4,
又由
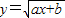
解x得:
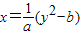
,
則
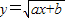
的反函數為
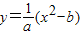
,
∵點(1,2)在反函數的圖象上
∴
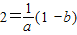
與a+b=4聯立解得:a=-3,b=7,
法二:由已知點(1,2)在
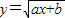
的圖象上
則
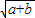
=2,即a+b=4,
又∵互為反函數的函數圖象關于y=x對稱
∴點(2,1)也在函數
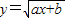
的圖象上
由此得:
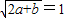
,即:2a+b=1,
將此與a+b=4聯立解得:a=-3,b=7,
ab=-21
答案:-21.
點評:本題方法二的解答,巧妙的利用了互為反函數的函數圖象間的關系,將點(1,2)和該點關于y=x的對稱點(2,1)分別代入原函數解析式構建方程組,過程簡捷,計算簡單,回避了求反函數的過程.這要比求出反函數,再將點的坐標代入方便得多,值得借鑒.

 的圖象上,又在它的反函數的圖象上,則ab= .
的圖象上,又在它的反函數的圖象上,則ab= . 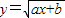 的圖象上,又在它的反函數的圖象上,可以有兩種方法求解:
的圖象上,又在它的反函數的圖象上,可以有兩種方法求解: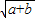 =2,即a+b=4,
=2,即a+b=4,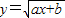 解x得:
解x得: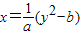 ,
,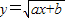 的反函數為
的反函數為 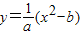 ,
,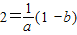
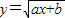 的圖象上
的圖象上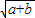 =2,即a+b=4,
=2,即a+b=4,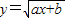 的圖象上
的圖象上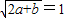 ,即:2a+b=1,
,即:2a+b=1,

 超能學典應用題題卡系列答案
超能學典應用題題卡系列答案