
【題目】已知![]() 的兩個頂點坐標是
的兩個頂點坐標是![]() ,
,![]() ,
,![]() 的周長為
的周長為![]() ,
,![]() 是坐標原點,點
是坐標原點,點![]() 滿足
滿足![]() .
.
(1)求點![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(2)若互相平行的兩條直線![]() ,
,![]() 分別過定點
分別過定點![]() 和
和![]() ,且直線
,且直線![]() 與曲線
與曲線![]() 交于
交于![]() 兩點,直線
兩點,直線![]() 與曲線
與曲線![]() 交于
交于![]() 兩點,若四邊形
兩點,若四邊形![]() 的面積為
的面積為![]() ,求直線
,求直線![]() 的方程.
的方程.
【答案】(1)![]() (2)
(2)![]() 或
或![]()
【解析】
(1)由![]() ,所以,可得點
,所以,可得點![]() 的軌跡是以
的軌跡是以![]() 為焦點的橢圓(不含左右頂點).再由
為焦點的橢圓(不含左右頂點).再由![]() 得得出點A的坐標與點M的坐標的關系,可求得點
得得出點A的坐標與點M的坐標的關系,可求得點![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(2)分直線![]() 的斜率不存在時和直線
的斜率不存在時和直線![]() 的斜率存在時兩種情況分別求解,當直線的斜率存在時,可設直線
的斜率存在時兩種情況分別求解,當直線的斜率存在時,可設直線![]() 的方程為
的方程為![]() ,直線
,直線![]() 的方程為
的方程為![]() 與曲線E的方程聯立求得邊
與曲線E的方程聯立求得邊![]() ,
,![]() ,
,![]() ,再由平行線間的距離可得平行四邊形的面積,可得解.
,再由平行線間的距離可得平行四邊形的面積,可得解.
(1)由已知,得![]() ,所以,點
,所以,點![]() 的軌跡是以
的軌跡是以![]() 為焦點的橢圓(不含左右頂點).
為焦點的橢圓(不含左右頂點).
因為,![]() ,
,![]() ,所以,
,所以,![]() ,
,![]() ,
,
所以,點![]() 的軌跡方程為
的軌跡方程為![]() .
.
設![]() ,
,![]() .由
.由![]() 得,
得,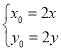 ,又
,又![]() .
.
故,點![]() 的軌跡
的軌跡![]() 的方程為
的方程為![]() ,即
,即![]() .
.
(2)由題意可知,當直線![]() 的斜率不存在時,易求得
的斜率不存在時,易求得![]() ,
,![]() ,
,
![]() ,
,![]() .這時,四邊形
.這時,四邊形![]() 的面積為
的面積為![]() ,不符合要求.
,不符合要求.
當直線![]() 的斜率存在時,可設直線
的斜率存在時,可設直線![]() 的方程為
的方程為![]() ,
,
則直線![]() 的方程為
的方程為![]()
由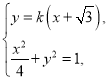 消去
消去![]() 得
得![]() ,
,
設![]() ,
,![]() ,則
,則![]() ,
,![]() .
.
故,![]() ,
,
又,兩條平行直線![]() ,
,![]() 間的距離
間的距離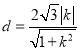 .
.
由橢圓的對稱性知:四邊形![]() 為平行四邊形,其面積
為平行四邊形,其面積![]() ,
,
解得,![]() 或
或![]() .
.
故,直線![]() 的方程為
的方程為![]() 或
或![]() .
.


 每日10分鐘口算心算速算天天練系列答案
每日10分鐘口算心算速算天天練系列答案科目:高中數學 來源: 題型:
【題目】某次知識競賽規則如下:在主辦方預設的7個問題中,選手若能連續正確回答出兩個問題,即停止答題,晉級下一輪.假設某選手正確回答每個問題的概率都是0.7,且每個問題的回答結果相互獨立,則該選手恰好回答了5個問題就晉級下一輪的概率等于( )
A.0.07497B.0.92503C.0.1323D.0.6174
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知雙曲線![]() :
: ![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,
, ![]() 為坐標原點,
為坐標原點, ![]() 是雙曲線上在第一象限內的點,直線
是雙曲線上在第一象限內的點,直線![]() 分別交雙曲線
分別交雙曲線![]() 左、右支于另一點
左、右支于另一點![]() ,
, ![]() ,且
,且![]() ,則雙曲線
,則雙曲線![]() 的離心率為( )
的離心率為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】第24屆冬奧會將于2022年2月4日至2月22日在北京市和河北省張家口市聯合舉行,這是中國歷史上第一次舉辦冬季奧運會.為了宣傳冬奧會,讓更多的人了解、喜愛冰雪項目,某校高三年級舉辦了冬奧會知識競賽(總分100分),并隨機抽取了![]() 名中學生的成績,繪制成如圖所示的頻率分布直方圖.已知前三組的頻率成等差數列,第一組和第五組的頻率相同.
名中學生的成績,繪制成如圖所示的頻率分布直方圖.已知前三組的頻率成等差數列,第一組和第五組的頻率相同.
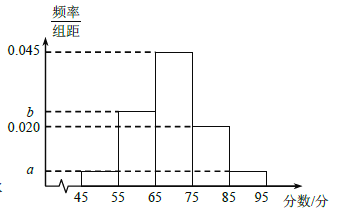
(Ⅰ)求實數![]() ,
,![]() 的值,并估計這
的值,并估計這![]() 名中學生的成績平均值
名中學生的成績平均值![]() ;(同一組中的數據用該組區間的中點值作代表)
;(同一組中的數據用該組區間的中點值作代表)
(Ⅱ)已知抽取的![]() 名中學生中,男女生人數相等,男生喜歡花樣滑冰的人數占男生人數的
名中學生中,男女生人數相等,男生喜歡花樣滑冰的人數占男生人數的![]() ,女生喜歡花樣滑冰項的人數占女生人數的
,女生喜歡花樣滑冰項的人數占女生人數的![]() ,且有95%的把握認為中學生喜歡花樣滑冰與性別有關,求
,且有95%的把握認為中學生喜歡花樣滑冰與性別有關,求![]() 的最小值.
的最小值.
參考數據及公式如下:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
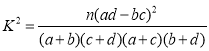 ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】十九大以來,某貧困地區扶貧辦積極貫徹落實國家精準扶貧的政策要求,帶領廣大農村地區人民群眾脫貧奔小康.經過不懈的奮力拼搏,新農村建設取得巨大進步,農民年收入也逐年增加,為了制定提升農民收入、實現2020年脫貧的工作計劃,該地扶貧辦統計了2019年50位農民的年收入并制成如下頻率分布直方圖:
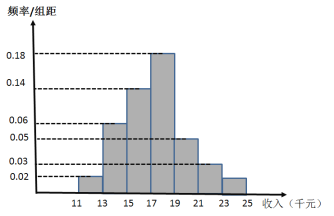
(1)根據頻率分布直方圖,估計50位農民的平均年收入![]() (單位:千元);(同一組數據用該組數據區間的中點值表示);
(單位:千元);(同一組數據用該組數據區間的中點值表示);
(2)由頻率分布直方圖,可以認為該貧困地區農民年收入X服從正態分布![]() ,其中
,其中![]() 近似為年平均收入
近似為年平均收入![]() ,
,![]() 近似為樣本方差
近似為樣本方差![]() ,經計算得
,經計算得![]() =6.92,利用該正態分布,求:
=6.92,利用該正態分布,求:
①在扶貧攻堅工作中,若使該地區約有占總農民人數的![]() 的農民的年收入高于扶貧辦制定的最低年收入標準,則最低年收入標準大約為多少千元?
的農民的年收入高于扶貧辦制定的最低年收入標準,則最低年收入標準大約為多少千元?
②為了調研“精準扶貧,不落一人”的政策要求落實情況,扶貧辦隨機走訪了1000位農民.若每位農民的年收入互相獨立,問:這1000位農民中的年收入不少于12.14千元的人數最有可能是多少?
附參考數據:![]() ,若隨機變量X服從正態分布
,若隨機變量X服從正態分布![]() ,則
,則![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com