已知函數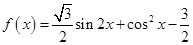
.
（1）求函數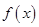
的最小正周期及在區間
的最大值；
（2）在
中，
、
、
所對的邊分別是
、
、
，
，
，求
周長
的最大值.
（1）最小正周期為
，在區間上的最大值為
；（2）
.
解析試題分析：（1）將函數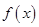 的解析式利用降冪公式與輔助角公式化簡為
，利用公式即可求出函數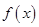的最小正周期，然后由
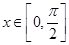求出
的取值范圍，根據圖象確定
的取值范圍，即可求出函數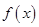在區間上的最大值；（2）先利用結合角
的取值范圍求出角的值，解法一是對邊利用余弦定理，借助基本不等式求出
的最大值，從而求出的最大值，解法二是利用正弦定理與內角和定理將轉化為以角
的三角函數，將轉化為求此函數在區間
的最大值.
（1）
，
所以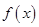最小正周期
，
，
，
最大值為；
（2）由得
又
，
解法一：
由余弦定理得, 
，
即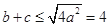
,
（當且僅當
時取等號）
所以
；
解法二：由正弦定理得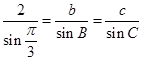
，即
，
，
所以
，
，
，
（當且僅當
時取最大值）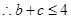
，
所以.
考點：1.降冪公式；2.正弦定理與余弦定理；3.三角函數的基本性質；4.基本不等式
科目：高中數學 來源： 題型：解答題
已知向量m＝(
sin 
，1)，n＝(cos ，cos2)．記f(x)＝m·n．
(1)若f(α)＝
，求cos(
－α)的值；
(2)在△ABC中，角A、B、C的對邊分別是a、b、c，且滿足(2a－c)cos B＝bcos C，若f(A)＝
，試判斷△ABC的形狀．
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
如圖，
是邊長為1的正三角形，
分別是邊
上的點，
段
過的重心
,設
.
（1）當
時，求
的長；
（2）分別記
的面積為
,試將表示為
的函數；
（3）求
的最大值和最小值。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
中，已知
，
，試判斷
中，
是角
對應的邊，向量
,
，且
．
；
的相鄰兩個極值的橫坐標分別為
、
，求
的單調遞減區間．
中，角
所對的邊分別為
，且
成等差數列．
的大小；
，求
邊上中線長的最小值．
中,角
所對的邊分別為
,且滿足
．
的大小;
取得最大值時,請判斷
，設函數
．
的單調遞增區間；
中，角
、
、
的對邊分別為
、
、
，且滿足
，
，求
的值．
中，角A、B、C的對邊分別為a、b、c，且角A、B、C成等差教列．
，求邊c的值；
，求t的最大值．