Question

已知動圓過定點P（1，0），且與定直線L:x=-1相切，點C在l上.

(1)求動圓圓心的軌跡M的方程；

（i）問：△ABC能否為正三角形？若能，求點C的坐標；若不能，說明理由

（ii）當△ABC為鈍角三角形時，求這種點C的縱坐標的取值范圍.

Answer 1

（1）y2=4x（2）不存在；當△ABC為鈍角三角形時，點C的縱坐標y的取值范圍是:

解析:

（1)依題意，曲線M是以點P為焦點，直線l為準線的拋物線，所以曲線M的方程為y2=4x.

假設存在點C（－1，y），使△ABC為正三角形，則|BC|=|AB|且|AC|=|AB|，即

   

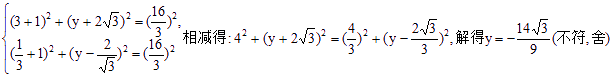
因此，直線l上不存在點C，使得△ABC是正三角形.

（ii）解法一：設C（－1，y）使△ABC成鈍角三角形，

，

，

∠CAB為鈍角.

.  

該不等式無解，所以∠ACB不可能為鈍角.

因此，當△ABC為鈍角三角形時，點C的縱坐標y的取值范圍是:

.

解法二： 以AB為直徑的圓的方程為:

.

當直線l上的C點與G重合時，∠ACB為直角，當C與G 點不重合，且A，

B，C三點不共線時， ∠ACB為銳角，即△ABC中∠ACB不可能是鈍角.

因此，要使△ABC為鈍角三角形，只可能是∠CAB或∠CBA為鈍角.

.

.

A，B，C三點共 線，不構成三角形.

因此，當△ABC為鈍角三角形時，點C的縱坐標y的取值范圍是：