
【題目】已知二次函數 ![]() 的最小值為0,不等式
的最小值為0,不等式 ![]() 的解集為
的解集為 ![]() .
.
(1)求集合 ![]() ;
;
(2)設集合 ![]() ,若集合
,若集合 ![]() 是集合
是集合 ![]() 的子集,求
的子集,求 ![]() 的取值范圍.
的取值范圍.
【答案】
(1)解:由二次函數 ![]() 的最小值是0得:
的最小值是0得: ![]() ,
, ![]() ,所以集合
,所以集合 ![]()
(2)解:當 ![]() 時,集合
時,集合 ![]() 符合題意;當
符合題意;當 ![]() 時,集合
時,集合 ![]() ,∴
,∴ ![]() ,∴
,∴ ![]() .綜上
.綜上 ![]() 的取值范圍是
的取值范圍是 ![]()
【解析】(1)利用二次函數的最小值求得b的值,再解得到的一元二次不等式即可得到集合A;(2)利用集合A與集合B的關系可以得知集合B包含于集合A,同時注意考慮集合B為空集時集合A,B的關系仍成立.
【考點精析】本題主要考查了解一元二次不等式的相關知識點,需要掌握求一元二次不等式![]()
![]() 解集的步驟:一化:化二次項前的系數為正數;二判:判斷對應方程的根;三求:求對應方程的根;四畫:畫出對應函數的圖象;五解集:根據圖象寫出不等式的解集;規律:當二次項系數為正時,小于取中間,大于取兩邊才能正確解答此題.
解集的步驟:一化:化二次項前的系數為正數;二判:判斷對應方程的根;三求:求對應方程的根;四畫:畫出對應函數的圖象;五解集:根據圖象寫出不等式的解集;規律:當二次項系數為正時,小于取中間,大于取兩邊才能正確解答此題.


 怎樣學好牛津英語系列答案
怎樣學好牛津英語系列答案 導學教程高中新課標系列答案
導學教程高中新課標系列答案科目:高中數學 來源: 題型:
【題目】設數列{an}的前n項和為Sn , 若點 ![]() 在函數f(x)=﹣x+c的圖象上運動,其中c是與x無關的常數,且a1=3.
在函數f(x)=﹣x+c的圖象上運動,其中c是與x無關的常數,且a1=3.
(1)求數列{an}的通項公式;
(2)記 ![]() ,求數列{bn}的前n項和Tn的最小值.
,求數列{bn}的前n項和Tn的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() 是數列
是數列![]() 的前n項和,
的前n項和,![]() ,且
,且![]() .
.
(1)求數列![]() 的通項公式;
的通項公式;
(2)對于正整數![]() ,已知
,已知![]() 成等差數列,求正整數
成等差數列,求正整數![]() 的值;
的值;
(3)設數列![]() 前n項和是
前n項和是![]() ,且滿足:對任意的正整數n,都有等式
,且滿足:對任意的正整數n,都有等式![]() 成立.求滿足等式
成立.求滿足等式![]() 的所有正整數n.
的所有正整數n.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】4月16日摩拜單車進駐大連市旅順口區,綠色出行引領時尚,旅順口區對市民進行“經常使用共享單車與年齡關系”的調查統計,若將單車用戶按照年齡分為“年輕人”(20歲~39歲)和“非年輕人”(19歲及以下或者40歲及以上)兩類,抽取一個容量為200的樣本,將一周內使用的次數為6次或6次以上的稱為“經常使用單車用戶”。使用次數為5次或不足5次的稱為“不常使用單車用戶”,已知“經常使用單車用戶”有120人,其中 ![]() 是“年輕人”,已知“不常使用單車用戶”中有
是“年輕人”,已知“不常使用單車用戶”中有 ![]() 是“年輕人”.
是“年輕人”.
(1)請你根據已知的數據,填寫下列 ![]() 列聯表:
列聯表:
年輕人 | 非年輕人 | 合計 | |
經常使用單車用戶 | |||
不常使用單車用戶 | |||
合計 |
(2)請根據(1)中的列聯表,計算 ![]() 值并判斷能否有
值并判斷能否有 ![]() 的把握認為經常使用共享單車與年齡有關?
的把握認為經常使用共享單車與年齡有關?
(附: ![]()
當 ![]() 時,有
時,有 ![]() 的把握說事件
的把握說事件 ![]() 與
與 ![]() 有關;當
有關;當 ![]() 時,有
時,有 ![]() 的把握說事件
的把握說事件 ![]() 與
與 ![]() 有關;當
有關;當 ![]() 時,認為事件
時,認為事件 ![]() 與
與 ![]() 是無關的)
是無關的)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在一段時間內有2000輛車通過高速公路上的某處,現隨機抽取其中的200輛進行車速統計,統計結果如右面的頻率分布直方圖所示.若該處高速公路規定正常行駛速度為90km/h~120 km/h,試估計2000輛車中,在這段時間內以正常速度通過該處的汽車約有( )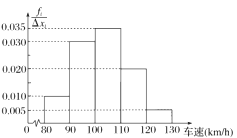
A.30輛
B.1700輛
C.170輛
D.300輛
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知全集U=R,集合A={x|x2﹣x﹣6≤0}, ![]() ,那么集合A∩(UB)=( )
,那么集合A∩(UB)=( )
A.[﹣2,4)
B.(﹣1,3]
C.[﹣2,﹣1]
D.[﹣1,3]
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com