
(2012年高考(廣東理))設數列![]() 的前
的前![]() 項和為
項和為![]() ,滿足
,滿足![]() ,
,![]()
![]() ,且
,且![]() 、
、![]() 、
、![]() 成等差數列.
成等差數列.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)求數列![]() 的通項公式;
的通項公式;
(Ⅲ)證明:對一切正整數![]() ,有
,有![]() .
.
解析:(Ⅰ)由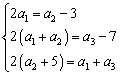 ,解得
,解得![]() .
.
(Ⅱ)由![]() 可得
可得![]() (
(![]() ),兩式相減,可得
),兩式相減,可得![]() ,即
,即![]() ,即
,即![]() ,所以數列
,所以數列![]() (
(![]() )是一個以
)是一個以![]() 為首項,3為公比的等比數列.由
為首項,3為公比的等比數列.由![]() 可得,
可得,![]() ,所以
,所以![]() ,即
,即![]() (
(![]() ),當
),當![]() 時,
時,![]() ,也滿足該式子,所以數列
,也滿足該式子,所以數列![]() 的通項公式是
的通項公式是![]() .
.
(Ⅲ)因為![]() ,所以
,所以![]() ,所以
,所以![]() ,于是
,于是 .
.
點評:上述證法實質上是證明了一個加強命題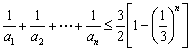 ,該加強命題的思考過程如下.
,該加強命題的思考過程如下.
考慮構造一個公比為![]() 的等比數列
的等比數列![]() ,其前
,其前![]() 項和為
項和為![]() ,希望能得到
,希望能得到![]() ,考慮到
,考慮到![]() ,所以令
,所以令![]() 即可.由
即可.由![]() 的通項公式的形式可大膽嘗試令
的通項公式的形式可大膽嘗試令![]() ,則
,則![]() ,于是
,于是![]() ,此時只需證明
,此時只需證明![]() 就可以了.
就可以了.
當然,![]() 的選取并不唯一,也可令
的選取并不唯一,也可令![]() ,此時
,此時![]() ,
,![]() ,與選取
,與選取![]() 不同的地方在于,當
不同的地方在于,當![]() 時,
時,![]() ,當
,當![]() 時,
時,![]() ,所以此時我們不能從第一項就開始放縮,應該保留前幾項,之后的再放縮,下面給出其證法.
,所以此時我們不能從第一項就開始放縮,應該保留前幾項,之后的再放縮,下面給出其證法.
當![]() 時,
時,![]() ;當
;當![]() 時,
時,![]() ;當
;當![]() 時,
時,![]() .
.
當![]() 時,
時,![]() ,所以
,所以
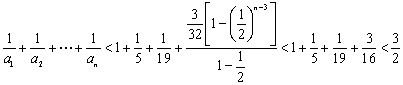 .
.
綜上所述,命題獲證.
下面再給出![]() 的兩個證法.
的兩個證法.
法1:(數學歸納法)
①當![]() 時,左邊
時,左邊![]() ,右邊
,右邊![]() ,命題成立.
,命題成立.
②假設當![]() (
(![]() ,
,![]()
![]() )時成立,即
)時成立,即![]() 成立.為了證明當
成立.為了證明當![]() 時命題也成立,我們首先證明不等式:
時命題也成立,我們首先證明不等式:![]() (
(![]() ,
,![]()
![]() ).
).
要證![]() ,只需證
,只需證![]() ,只需證
,只需證![]() ,只需證
,只需證![]() ,只需證
,只需證![]() ,該式子明顯成立,所以
,該式子明顯成立,所以![]() .
.
于是當![]() 時,
時,![]() ,所以命題在
,所以命題在![]() 時也成立.
時也成立.
綜合①②,由數學歸納法可得,對一切正整數![]() ,有
,有![]() .
.
備注:不少人認為當不等式的一邊是常數的時候是不能用數學歸納法的,其實這是一個錯誤的認識.
法2:(裂項相消法)(南海中學錢耀周提供)
當![]() 時,
時,![]() 顯然成立.當
顯然成立.當![]() 時,
時,![]() 顯然成立.
顯然成立.
當![]() 時,
時,![]()
![]()
![]() ,又因為
,又因為![]() ,所以
,所以![]() (
(![]() ),所以
),所以![]() (
(![]() ),所以
),所以
![]() .
.
綜上所述,命題獲證.


湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com