
【題目】已知函數 f(x)是定義在 R上的偶函數,當 x≥0 時,f(x)=x2+ax+b 的部分圖象如圖所示:

(1)求 f(x)的解析式;
(2)在網格上將 f(x)的圖象補充完整,并根據 f(x)圖象寫出不等式 f(x)≥1的解集.
【答案】(1)f(x)=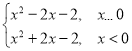 ;(2)(﹣∞,﹣3]∪[3,+∞)
;(2)(﹣∞,﹣3]∪[3,+∞)
【解析】
(1)根據函數圖像,將![]() 代入解二元一次方程即可求得解析式
代入解二元一次方程即可求得解析式
(2)結合圖像![]() ,采用數形結合的方法,當f(x)的圖像在
,采用數形結合的方法,當f(x)的圖像在![]() 上方時,即可求得x的取值范圍
上方時,即可求得x的取值范圍
(1)由題意知f(0)=﹣2,f(1)=﹣3,即![]() 得a=﹣2,b=﹣2,
得a=﹣2,b=﹣2,
即當x≥0時,f(x)=x2﹣2x﹣2.∵f(x)是偶函數,
∴當x<0時,﹣x>0,則f(﹣x)=x2+2x﹣2=f(x),即f(x)=x2+2x﹣2,x<0,
即f(x)=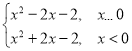 .
.
(2)對應圖象如圖:當f(x)=1時,得x=3或x=﹣3,若f(x)≥1,得x≥3或x≤﹣3,
即不等式的解集為:(﹣∞,﹣3]∪[3,+∞)
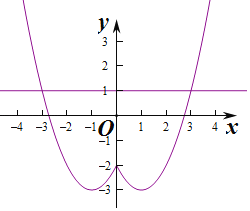


科目:高中數學 來源: 題型:
【題目】已知Sn為等差數列{an}的前n項和,S6=51,a5=13.
(1)求數列{an}的通項公式;
(2)數列{bn}的通項公式是bn=![]() , 求數列{bn}的前n項和Sn .
, 求數列{bn}的前n項和Sn .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】![]() 年
年![]() 月
月![]() 日是第二十七屆“世界水日”,
日是第二十七屆“世界水日”,![]() 月
月![]() 日是第三十二屆“中國水周”.我國紀念
日是第三十二屆“中國水周”.我國紀念![]() 年“世界水日”和“中國水周”活動的宣傳主題為“堅持節水優先,強化水資源管理”.某中學課題小組抽取
年“世界水日”和“中國水周”活動的宣傳主題為“堅持節水優先,強化水資源管理”.某中學課題小組抽取![]() 、
、![]() 兩個小區各
兩個小區各![]() 戶家庭,記錄他們
戶家庭,記錄他們![]() 月份的用水量(單位:
月份的用水量(單位:![]() )如下表:
)如下表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1)根據兩組數據完成下面的莖葉圖,從莖葉圖看,哪個小區居民節水意識更好?
|
| |
| ||
| ||
| ||
|
(2)從用水量不少于![]() 的家庭中,
的家庭中,![]() 、
、![]() 兩個小區各隨機抽取一戶,求
兩個小區各隨機抽取一戶,求![]() 小區家庭的用水量低于
小區家庭的用水量低于![]() 小區的概率.
小區的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系中,以原點為極點, ![]() 軸的正半軸為極軸建立極坐標系,已知曲線
軸的正半軸為極軸建立極坐標系,已知曲線![]() :
:![]() ,已知過點
,已知過點![]() 的直線
的直線![]() 的參數方程為:
的參數方程為: (
(![]() 為參數),直線
為參數),直線![]() 與曲線
與曲線![]() 分別交于
分別交于![]() 兩點.
兩點.
(1)寫出曲線![]() 和直線
和直線![]() 的普通方程;
的普通方程;
(2)若![]() ,
,![]() ,
,![]() 成等比數列,求
成等比數列,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知 ![]() =(cosα,sinα),
=(cosα,sinα), ![]() =(cosβ,sinβ),0<β<α<π.
=(cosβ,sinβ),0<β<α<π.
(1)若| ![]() ﹣
﹣ ![]() |=
|= ![]() ,求證:
,求證: ![]() ⊥
⊥ ![]() ;
;
(2)設 ![]() =(0,1),若
=(0,1),若 ![]() +
+ ![]() =
= ![]() ,求α,β的值.
,求α,β的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設![]() ,
,![]() 為兩條不同的直線,
為兩條不同的直線,![]() ,
,![]() 為兩個不同的平面,給出下列命題:
為兩個不同的平面,給出下列命題:
①若![]() ,
,![]() ,則
,則![]() ;
;
②若![]() ,
,![]() ,則
,則![]() ;
;
③若![]() ,
,![]() ,
,![]() ,則
,則![]() ;
;
④若![]() ,
,![]() ,則
,則![]() 與
與![]() 所成的角和
所成的角和![]() 與
與![]() 所成的角相等.
所成的角相等.
其中正確命題的序號是( )
A.①②B.①④C.②③D.②④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知某三棱錐的三視圖如圖所示,圖中的3個直角三角形的直角邊長度已經標出,則在該三棱錐中,最短的棱和最長的棱所在直線的成角余弦值為( ) 
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,曲線C1的參數方程為 ![]() (α為參數);在以O為極點,x軸正半軸為極軸的極坐標系中,曲線C2的極坐標方程為ρcos2θ=sinθ.
(α為參數);在以O為極點,x軸正半軸為極軸的極坐標系中,曲線C2的極坐標方程為ρcos2θ=sinθ.
(Ⅰ)求C1的普通方程和C2的直角坐標方程;
(Ⅱ)若射線l:y=kx(x≥0)分別交C1 , C2于A,B兩點(A,B異于原點).當 ![]() 時,求|OA||OB|的取值范圍.
時,求|OA||OB|的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com