
三次函數當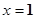 時有極大值
時有極大值 ,當
,當 時有極小值
時有極小值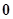 ,且函數過原點,則此函數是( )
,且函數過原點,則此函數是( )
A. B.
B.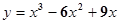
C.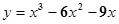 D.
D.
B
【解析】
試題分析:本題是據題意求參數的題,題目中x=1時有極大值4,當x=3時有極小值0,且函數圖象過原點,可轉化出五個等式,則其四建立方程.解:f’(x)=3a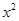 +2bx+c(a≠0),∵x=1時有極大值4,當x=3時有極小值0,∴f’(1)="3a+2b+c=0"
①f’(3)="27a+6b+c=0"
②f(1)="a+b+c+d=4"
③又函數圖象過原點,所以 d="0" ④,①②③④聯立得 a=1,b=-6,c=9,故函數f(x)=
+2bx+c(a≠0),∵x=1時有極大值4,當x=3時有極小值0,∴f’(1)="3a+2b+c=0"
①f’(3)="27a+6b+c=0"
②f(1)="a+b+c+d=4"
③又函數圖象過原點,所以 d="0" ④,①②③④聯立得 a=1,b=-6,c=9,故函數f(x)=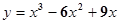 ,故選B.
,故選B.
考點:導數的運用
點評:本小題考點是導數的運用,考查導數與極值的關系,本題的特點是用導數一極值的關建立方程求參數---求函數的表達式


 小學教材完全解讀系列答案
小學教材完全解讀系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com