分析:(Ⅰ)設
M(a,y1),N(a,y2),根據題意由
•=0得
y1y2=-a2<0,由
||=||=2,得
=2,
=2,由此可以求出a,b的值.
(Ⅱ)|MN|
2=(y
1-y
2)
2=y
12+y
22-2y
1y
2≥-2y
1y
2-2y
1y
2=-4y
1y
2=6a
2.當且僅當
y1=-y2=a或
y2=-y1=a時,|MN|取最小值
a,由能夠推導出
+與
共線.
解答:解:由a
2-b
2=c
2與
e==,得a
2=2b
2,
F1(-a,0),F2(a,0),l的方程為
x=a設
M(a,y1),N(a,y2)則
=(a,y1),=(a,y2)由
•=0得
y1y2=-a2<0①
(Ⅰ)由
||=||=2,得
=2②
=2③
由①、②、③三式,消去y
1,y
2,并求得a
2=4
故
a=2,b==(Ⅱ)證明:|MN|
2=(y
1-y
2)
2=y
12+y
22-2y
1y
2≥-2y
1y
2-2y
1y
2=-4y
1y
2=6a
2當且僅當
y1=-y2=a或
y2=-y1=a時,|MN|取最小值
a此時,
+=(a,y1)+(a,y2)=(2a,y1+y2)=(2a,0)=2故
+與
共線.
點評:此題重點考查橢圓中的基本量的關系,進而求橢圓待定常數,考查向量的綜合應用;熟悉橢圓各基本量間的關系,數形結合,熟練地進行向量的坐標運算,設而不求消元的思想在圓錐曲線問題中的靈活應用.

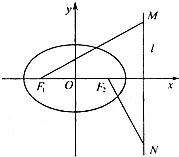 設橢圓
設橢圓

 舉一反三單元同步過關卷系列答案
舉一反三單元同步過關卷系列答案