
【題目】已知二次函數(shù)![]() 的對(duì)稱軸為
的對(duì)稱軸為![]() ,
,![]() .
.
(1)求函數(shù)![]() 的最小值及取得最小值時(shí)
的最小值及取得最小值時(shí)![]() 的值;
的值;
(2)試確定![]() 的取值范圍,使
的取值范圍,使![]() 至少有一個(gè)實(shí)根;
至少有一個(gè)實(shí)根;
(3)當(dāng)![]() 時(shí),
時(shí),![]() ,對(duì)任意
,對(duì)任意![]() 有
有![]() 恒成立,求
恒成立,求![]() 的取值范圍.
的取值范圍.
【答案】(1)![]() ,此時(shí)
,此時(shí)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
試題分析:(1)由![]() ,則
,則![]() ,利用基本不等式,即可求解函數(shù)
,利用基本不等式,即可求解函數(shù)![]() 的最小值及取得最小值時(shí)
的最小值及取得最小值時(shí)![]() 的值;(2)根據(jù)二次函數(shù)的性質(zhì),可得
的值;(2)根據(jù)二次函數(shù)的性質(zhì),可得![]() ,使得
,使得![]() ,即可求解
,即可求解![]() 的取值范圍;(3)由
的取值范圍;(3)由![]() ,
,![]() 恒成立,即
恒成立,即![]() ,令
,令![]() ,則
,則![]() ,利用基本不等式求得最值,即可
,利用基本不等式求得最值,即可![]() 的取值范圍.
的取值范圍.
試題解析:(1)∵![]() ,∴
,∴![]() ,
,
∴![]() ,當(dāng)且僅當(dāng)
,當(dāng)且僅當(dāng)![]() ,即
,即![]() 時(shí)“
時(shí)“![]() ”成立,即
”成立,即![]() ,此時(shí)
,此時(shí)![]() .
.
(2)![]() 的對(duì)稱軸為
的對(duì)稱軸為![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
![]() 至少有一實(shí)根,∴
至少有一實(shí)根,∴![]() 至少有一實(shí)根,
至少有一實(shí)根,
即![]() 與
與![]() 的圖象在
的圖象在![]() 上至少有一個(gè)交點(diǎn),
上至少有一個(gè)交點(diǎn),
![]() ,∴
,∴![]() ,
,![]() ,
,
∴![]() ,∴
,∴![]() ,∴
,∴![]() 的取值范圍為
的取值范圍為![]() .
.
(3)因?yàn)?/span>![]() ,∴
,∴![]()
![]() ,
,
∴![]() ,
,![]() 恒成立,∴
恒成立,∴![]() ,
,
令![]() ,
,![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
令![]() ,設(shè)
,設(shè)![]() ,
,![]() 為
為![]() 上任意兩不等實(shí)數(shù),且
上任意兩不等實(shí)數(shù),且![]() ,
,
∴![]()
![]() ,
,
∵![]() ,∴
,∴![]() ,
,![]() ,∴
,∴![]() ,
,
∴![]() 在
在![]() 上單調(diào)遞增,∴
上單調(diào)遞增,∴![]() ,∴
,∴![]() ,
,
∴![]() 的取值范圍為
的取值范圍為![]() .
.


 靈星計(jì)算小達(dá)人系列答案
靈星計(jì)算小達(dá)人系列答案 孟建平錯(cuò)題本系列答案
孟建平錯(cuò)題本系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】選修4-1《幾何證明選講》
已知A、B、C、D為圓O上的四點(diǎn),直線DE為圓O的切線,AC∥DE,AC與BD相交于H點(diǎn)

(1)求證:BD平分∠ABC;
(2)若AB=4,AD=6,BD=8,求AH的長(zhǎng).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在三棱柱![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 為線段
為線段![]() 上一點(diǎn).
上一點(diǎn).
(Ⅰ)求![]() 的值,使得
的值,使得![]() 平面
平面![]() ;
;
(Ⅱ)在(Ⅰ)的條件下,求二面角![]() 的正切值.
的正切值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)![]() 實(shí)數(shù)
實(shí)數(shù)![]() 滿足不等式
滿足不等式![]() 函數(shù)
函數(shù)![]() 無極值點(diǎn).
無極值點(diǎn).
(1)若“![]() ”為假命題,“
”為假命題,“![]() ”為真命題,求實(shí)數(shù)
”為真命題,求實(shí)數(shù)![]() 的取值范圍;
的取值范圍;
(2)已知“![]() ”為真命題,并記為
”為真命題,并記為![]() ,且
,且![]() ,若
,若![]() 是
是![]() 的必要不充分條件,求正整數(shù)
的必要不充分條件,求正整數(shù)![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知a,b,c是兩兩不等的實(shí)數(shù),則p=a2+b2+c2與q=ab+bc+ca的大小關(guān)系是________.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知圓![]() (
(![]() )的圓心為點(diǎn)
)的圓心為點(diǎn)![]() ,直線
,直線![]() :
:![]() .
.
(1)若![]() ,求直線
,求直線![]() 被圓
被圓![]() 所截得弦長(zhǎng)的最大值;
所截得弦長(zhǎng)的最大值;
(2)若直線![]() 是圓心
是圓心![]() 下方的切線,當(dāng)
下方的切線,當(dāng)![]() 在
在![]() 上變化時(shí),求
上變化時(shí),求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某學(xué)校為加強(qiáng)學(xué)生的交通安全教育,對(duì)學(xué)校旁邊![]() ,
,![]() 兩個(gè)路口進(jìn)行了8天的檢測(cè)調(diào)查,得到每天各路口不按交通規(guī)則過馬路的學(xué)生人數(shù)(如莖葉圖所示),且
兩個(gè)路口進(jìn)行了8天的檢測(cè)調(diào)查,得到每天各路口不按交通規(guī)則過馬路的學(xué)生人數(shù)(如莖葉圖所示),且![]() 路口數(shù)據(jù)的平均數(shù)比
路口數(shù)據(jù)的平均數(shù)比![]() 路口數(shù)據(jù)的平均數(shù)小2.
路口數(shù)據(jù)的平均數(shù)小2.
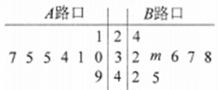
(1)求出![]() 路口8個(gè)數(shù)據(jù)中的中位數(shù)和莖葉圖中
路口8個(gè)數(shù)據(jù)中的中位數(shù)和莖葉圖中![]() 的值;
的值;
(2)在![]() 路口的數(shù)據(jù)中任取大于35的2個(gè)數(shù)據(jù),求所抽取的兩個(gè)數(shù)據(jù)中至少有一個(gè)不小于40的概率.
路口的數(shù)據(jù)中任取大于35的2個(gè)數(shù)據(jù),求所抽取的兩個(gè)數(shù)據(jù)中至少有一個(gè)不小于40的概率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在互聯(lián)網(wǎng)時(shí)代,網(wǎng)校培訓(xùn)已經(jīng)成為青年學(xué)習(xí)的一種趨勢(shì),假設(shè)某網(wǎng)校的套題每日的銷售量![]() (單位:千套)與銷售價(jià)格
(單位:千套)與銷售價(jià)格![]() (單位:元/套)滿足的關(guān)系式
(單位:元/套)滿足的關(guān)系式![]() (
(![]() ,
,![]() 為常數(shù)),其中
為常數(shù)),其中![]() 與
與![]() 成反比,
成反比,![]() 與
與![]() 的平方成正比,已知銷售價(jià)格為5元/套時(shí),每日可售出套題21千套,銷售價(jià)格為3.5元/套時(shí),每日可售出套題69千套.
的平方成正比,已知銷售價(jià)格為5元/套時(shí),每日可售出套題21千套,銷售價(jià)格為3.5元/套時(shí),每日可售出套題69千套.
(1) 求![]() 的表達(dá)式;
的表達(dá)式;
(2) 假設(shè)網(wǎng)校的員工工資,辦公等所有開銷折合為每套題3元(只考慮銷售出的套數(shù)),試確定銷售價(jià)格![]() 的值,使網(wǎng)校每日銷售套題所獲得的利潤(rùn)最大.(保留1位小數(shù))
的值,使網(wǎng)校每日銷售套題所獲得的利潤(rùn)最大.(保留1位小數(shù))
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,點(diǎn)E為正方形ABCD邊CD上異于點(diǎn)C,D的動(dòng)點(diǎn),將△ADE沿AE翻折成△SAE,使得平面SAE⊥平面ABCE,則下列說法中正確的有( )
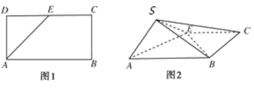
①存在點(diǎn)E使得直線SA⊥平面SBC;
②平面SBC內(nèi)存在直線與SA平行
③平面ABCE內(nèi)存在直線與平面SAE平行;
④存在點(diǎn)E使得SE⊥BA.
A.1個(gè) B.2個(gè) C.3個(gè) D.4個(gè)
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com