
(2005
廣東,19)設函數f(x)在(-∞,+∞)上滿足f(2-x)=f(2+x),f(7-x)=f(7+x),且在閉區間[0,7]上,只有f(1)=f(3)=0;(1)
試判斷函數y=f(x)的奇偶性;(2)
試求方程f(x)=0在閉區間[-2005,2005]上的根的個數,并證明你的結論.|
解析:解法一: (1)若f(x)是偶函數,則f(-x)=f(2-(x+2))=f(2+(2+x))=f(4+x)=f(x),于是有f(7)=f(3)=0,這與f(x)在[0,7]上只有f(1)=f(3)=0矛盾!故f(x)不是偶函數.若 f(x)是奇函數,則f(0)=f(-0)=-f(0),有f(0)=0,這與在[0,7]上只有f(1)=f(3)=0矛盾!∴f(x)不是奇函數.故f(x)既不是偶函數,也不是奇函數.(2)∵f(x)=f[2 +(x-2)]=f[2-(x-2)]=f(4-x),f(x)=f[7 +(x-7)]=f[7-(x-7)]=f(14-x).∴f(14 -x)=f(4-x),即f[10+(4-x)]=f(4-x).∴f(x +10)=f(x).∴f(x)=f(x+10n),n Z. Z.
因此, f(1)=f(1+10n)=0,f(3)=f(3+10n)=0.即 x=10n+1和x=10n+3(n Z)均是f(x)=0的根. Z)均是f(x)=0的根.
由- 2005≤10n+1≤2005和-2005≤10n+3≤2005及n Z可得:n=0,±1,……,±200. Z可得:n=0,±1,……,±200.
故方程 f(x)=0在[-2005,2005]上的根至少有802個.如果存在 c (7,10)使f(c)=0,則f(14-c)=f(c)=0. (7,10)使f(c)=0,則f(14-c)=f(c)=0.
但 7>14-c≥4,這與f(x)在[0,7]上只有f(1)=f(3)=0矛盾!故f(x)=0在[0,10]上只有兩個根,即x=1和x=3.設 d是f(x)=0在區間[-2005,2005]上任意一個根,則存在整數 n使d=10n+a,a [0,10], [0,10],
且 f(d)=f(10n+a)=f(a)=0.由上可知 a=1或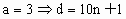 或d=10n+3. 或d=10n+3.
所以 f(x)=0在[-2005,2005]上有且僅有802個根.解法二: (1)∵f(x)在[0,7]上只有f(1)=f(3)=0.∴f(0) ≠0,即f(x)不是奇函數.∵f(2 -x)=f(2+x),f(x)關于x=2對稱.∴f( -1)=f(5).而 f(5)≠0 f(1)≠f(-1),即f(x)不是偶函數. f(1)≠f(-1),即f(x)不是偶函數.
故 f(x)是非奇非偶函數.(2) 由f(x)=f[2-(2-x)]=f[2+(2-x)]=f(4-x),有 f(x)=f[7-(3+x)]=f[7+(3+x)]=f(x+10).即 f(x)是周期為10的周期函數.∴f(7 -x)=f(7+x),∴f(x)關于x=7對稱.∵f(x) 在[0,7]上僅有f(1)=f(3)=0,∴f(x) 在(7,10)上沒有根.即 f(x)在[0,10]上僅x=1和x=3兩個根.于是 f(x)在[0,2000]內僅有400個根,在[2000,2005]上僅有2根,在[-2000,0]內僅有400個根,而在[-2005,-2000]上沒有根.故 f(x)在[-2005,2005]內僅有802個根. |
|
剖析:本小題主要考查函數的奇偶性、方程的根、解不等式等基礎知識,以及函數與方程、分類與整合、化歸與轉化的數學思想方法,考查思維能力、運算能力. |


 智慧小復習系列答案
智慧小復習系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com